Similar Questions
Explore conceptually related problems
Recommended Questions
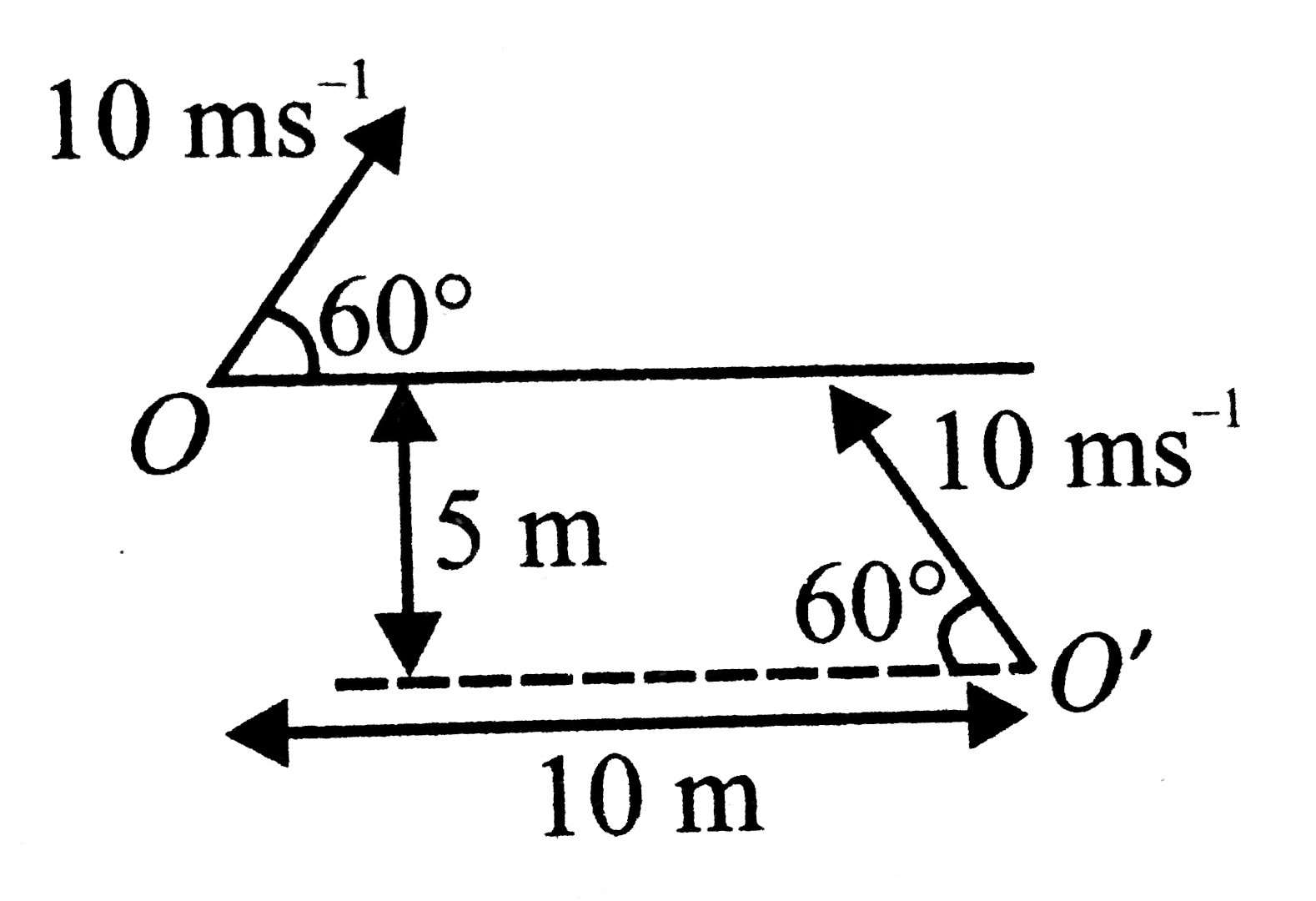
- Two particles are projected simultaneously from two points O and O' su...
Text Solution
|
- Two particles are located on a horizontal plane at a distance 60 m. At...
Text Solution
|
- Two particles are separated at a horizontal distance x as shown in (Fi...
Text Solution
|
- Two particles are projected simultaneously from two points O and O' su...
Text Solution
|
- A particle is projected from a point O with an initial speed of 30 ms^...
Text Solution
|
- Two particles are projected simultaneously from two points, O and O' s...
Text Solution
|
- A particle is projected vertically upwards from O with a velocity and ...
Text Solution
|
- Two particles are projected with speed 4 m//s and 3 m//s simultaneousl...
Text Solution
|
- Two particles are projected simultaneously with same speed V0 in same...
Text Solution
|