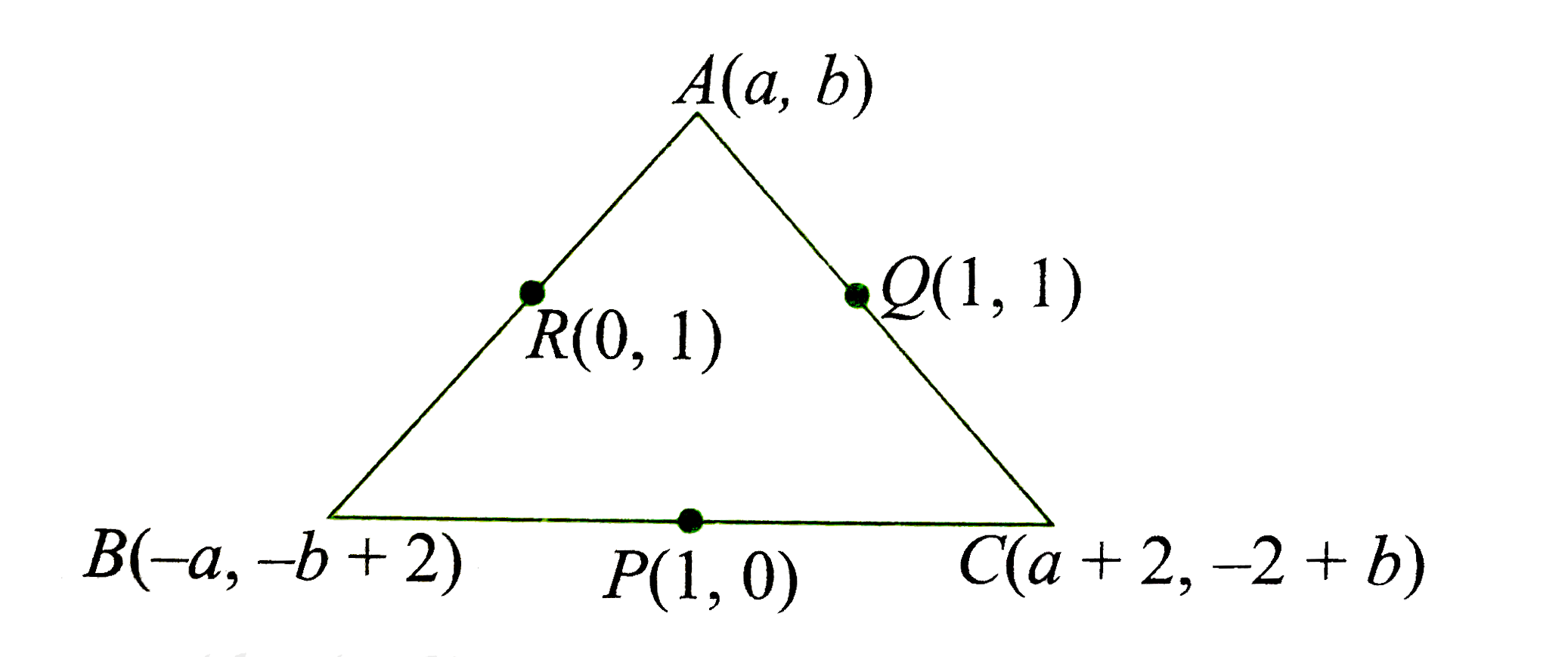
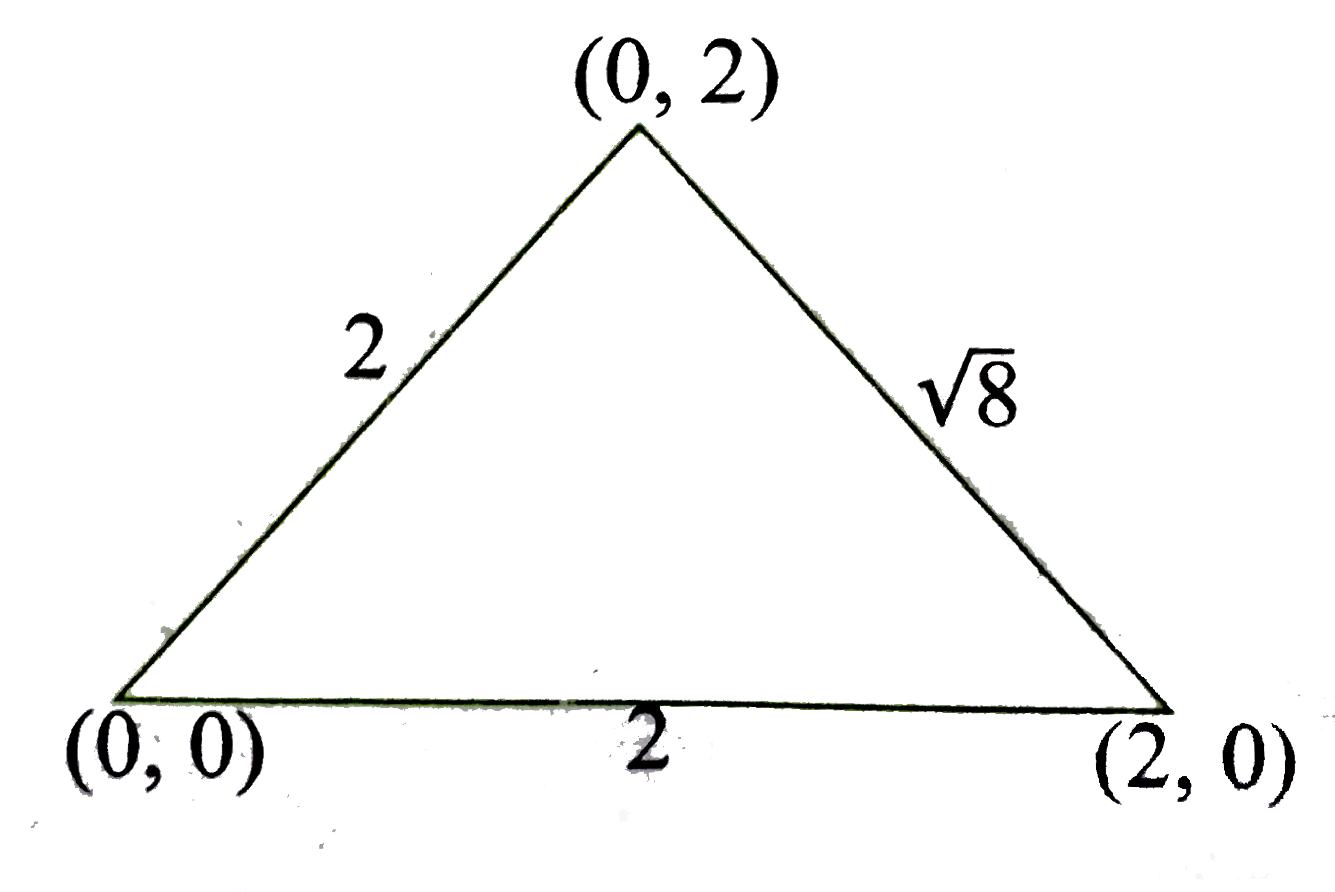
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The x-coordiante of the incentre of the triangle that has the coordian...
Text Solution
|
- If mid-points of the sides of Delta ABC are (1,2),(0,1) and (1,0), the...
Text Solution
|
- If mid-points of the sides of Delta ABC are (1,2),(0,1) and (1,0), the...
Text Solution
|
- If the incentre of an equilateral triangle is (1,1) and the equation o...
Text Solution
|
- If [(2,1),(3,2)] A[(-3,2),(5,-3)]=[(1,0),(0,1)] then a is equal to (A)...
Text Solution
|
- If A=[(0,1),(1,0)] then A^4 is (A) [(0,0),(1,1)] (B) [(1,1),(0,0)] (C)...
Text Solution
|
- If A=[(1,0),(0,1)] then A^4= (A) [(1,0),(0,1)] (B) [(1,1),(0,10)] (C) ...
Text Solution
|
- The coordiantes of a point are the perpendicular distance from the ….....
Text Solution
|
- The coordianted beating of cilia is
Text Solution
|