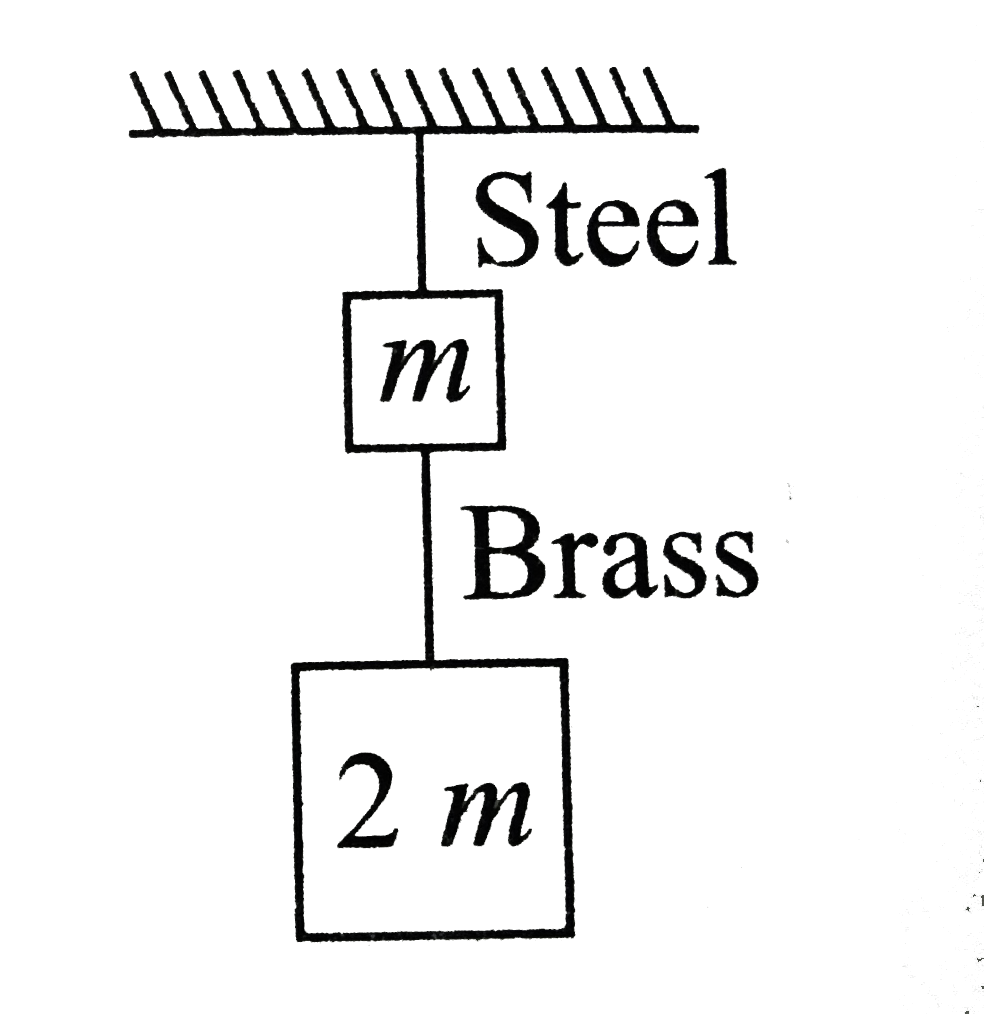Similar Questions
Explore conceptually related problems
Recommended Questions
- If the ratio of lengths, radii and Young's moduli of steel and brass w...
Text Solution
|
- If the ratio of lengths, radii and Young's moduli of steel and brass w...
Text Solution
|
- If the ratio of lenghts, radi and Young's moduli of steel and brass wi...
Text Solution
|
- If the ratio of lengths, radii and youngs's modulus of steel and and b...
Text Solution
|
- If the ratio of lengths, radii and Young's moduli of steel and brass w...
Text Solution
|
- If the ratio of diameters,lengths and Young's moduli of steel and bras...
Text Solution
|
- If the ratio of lengths, radii and young's modulii of steel and brass ...
Text Solution
|
- The Young's modulii of brass ans steel are in the ratio of 1 : 2. A br...
Text Solution
|
- If the ratio of lengths, radii and Young's modulus of steel and brass ...
Text Solution
|