In a horizontal unifrom electirc field, a small charged disk is gently released on the top of a fixed sperical dome. The disk slides down the some without friction and breaks away from the surface of the dome at the angular position `theta = sin^(-1)(3//5)` from verical. Determine the ration of the force of gravity acting on the disk to force of its interaction with the field .
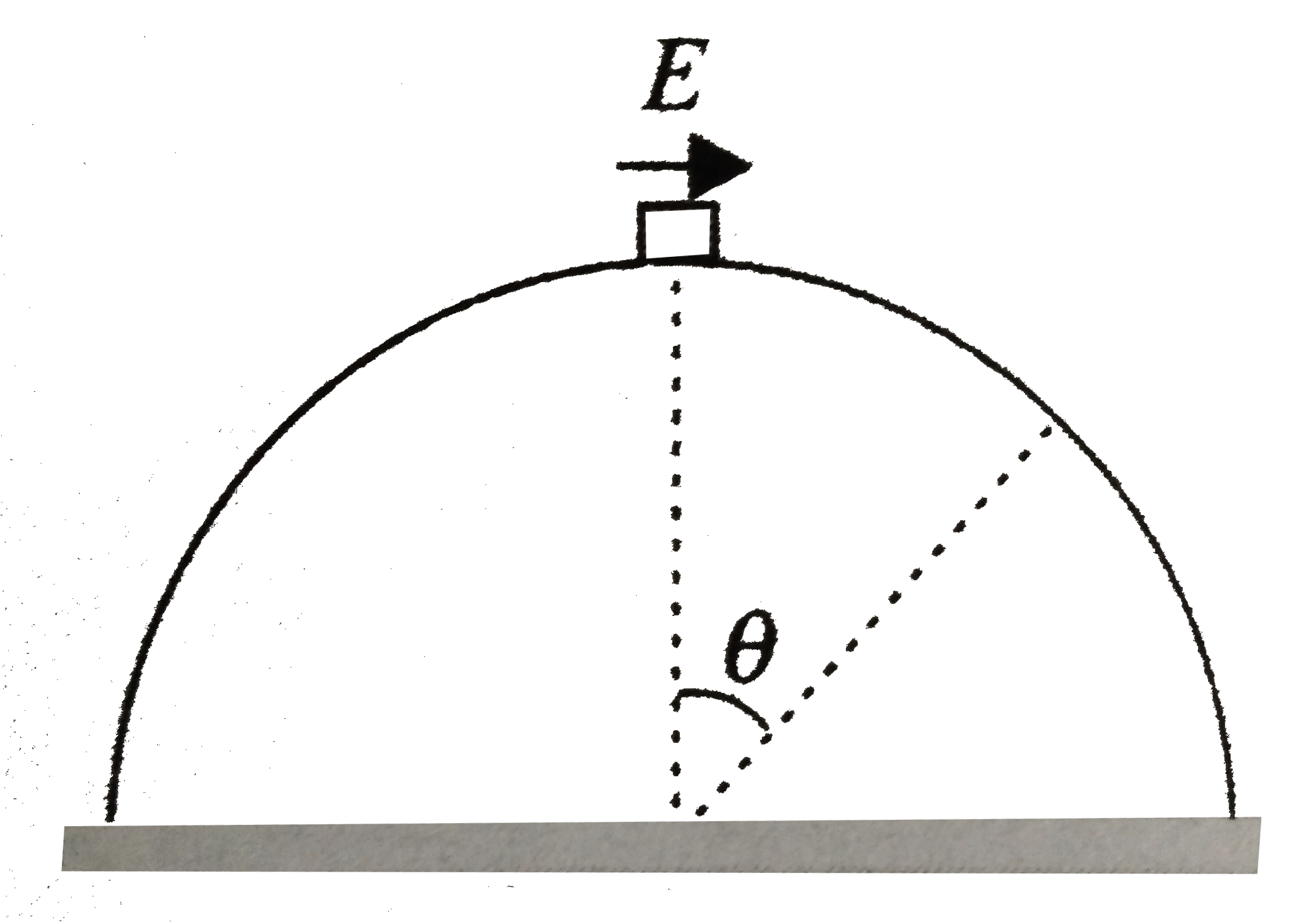
In a horizontal unifrom electirc field, a small charged disk is gently released on the top of a fixed sperical dome. The disk slides down the some without friction and breaks away from the surface of the dome at the angular position `theta = sin^(-1)(3//5)` from verical. Determine the ration of the force of gravity acting on the disk to force of its interaction with the field .


Similar Questions
Explore conceptually related problems
A samll object of mass 10.0 g is at rest 30.0 cm from a horizontal disk's centre. The disk starts to rotate from rest about its centre with a constant angular acceleration of 4.50 rad/ s^(2) . What is the magnitude of the net force acting on the object after a time of t=1/3 s if the object remains at rest with respect to the disk ?
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
Take a small stone. Hold it in your hand. We know that the force gravity due to the earth acts on each and every object. When we were holding the stone in our hand, the stone was experiencing this force, but it was balanced by a force that we were applying on it in the opposite direction. As a result, the stone remained at rest. Once we release the stone from our hands the only force that acts on it is the gravitational force of the earth and the stone falls down under its influence. Whenever an object moves under the influence of the force of gravity alone, it is said to be falling freely. Thus the released stone is in a free fall. In free fall, the initial velocity of the object is zero and goes on increasing due to acceleration due to gravity of the earth. During free fall, the frictional force due to air opposes the motion of the object and a buoyant force also acts on the object. Thus, true free fall is possible only in vacuum. For a freely falling object, the velocity on reaching the earth and the time taken for it can be calculated by using Newton's equations of motion. For free fall the initial velocity u=0 and the acceleration a=g . Thus, we can write the equations as v="gt",s=1/2"gt"^(2),v^(2)=2gs For calculating the motion of an object thrown upwards, acceleration is negative, i.e. in a direction opposite to the velocity and is taken to be -g. The magnitude of g is the same but the velocity of the object decreases due to -ve acceleration. The moon and the artificial satellites are moving only under the influence of the gravitational field of the earth. Thus they are in free fall. Which force acts on the stone in free fall after you release it?
Take a small stone. Hold it in your hand. We know that the force gravity due to the earth acts on each and every object. When we were holding the stone in our hand, the stone was experiencing this force, but it was balanced by a force that we were applying onn it in the opposite direction. As a result, the stone remained at rest. Once we release the stone from our hands the only force that acts onit is the gravitational force of the earth and the stone falls down under its influence. Whenever an object moves under the influence of the force of gravity alone, it is said to be falling freely. Thus the released stone is in a free fall. In free fall, the initial velocity of the object is zero and goes on increasing due toi acceleration due to gravity of the earth. During free fall, the frictional force due to air opposes the motion of the object anda buoyant force also acts on the object. Thus, true free fall is posible only in vacuum. For a freely falling object, the velocity on reachign the earth and the time taken for it can be calculated by using Newton's eqwuations of motion. For free fall the initial velocity u=0 and the acceleration a=g . Thus, we can write the equations as v="gt",s=1/2"gt"^(2),v^(2)=2gs For calculating the motion of an object thrown upwards, acceleration is negative, i.e. in a direction opposite ot the velocity and is taken to be -g. The magnitude of g is the same but the velocity of the object decreases due to -ve acceleration. The moon and the artificial satellites are moving only under the influence of the gravitational field of the earth. Thus they are in free fall. Which force acts on the stone when held in the hand?
Two thin rings of slightly different radii are joined together to make a wheel (see figure) of radius R. There is a very small smooth gap between the two ring. The wheel has a mass M and its centre of mass is at its geometrical centre. The wheel stands on a smooth surface and a small particle of mass m lies at the top (A) in the gap between the rings. The system is released and the particle begins to slide down along the gap. Assume that the ring does not lose contact with the surface. (a) As the particle slides down from top point A to the bottom point B, in which direction does the centre of the wheel move? (b) Find the speed of centre of the wheel when the particle just reaches the bottom point B. How much force the particle is exerting on the wheel at this instant? (c) Find the speed of the centre of the wheel at the moment the position vector of the particle with respect to the centre of the wheel makes an angle q with the vertical. Do this calculation assuming that the particle is in contact with the inner ring at desired value of theta
In the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B . Find the maximum force exerted by track on the sphere during its motion.
In the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B . Find the maximum force exerted by track on the sphere during its motion.
Recommended Questions
- In a horizontal unifrom electirc field, a small charged disk is gently...
Text Solution
|
- A uniform thin cylindrical disk of mass M and radius R is attaached to...
Text Solution
|
- Two disks of masses m(1) and m(2) are connected by a spring of force c...
Text Solution
|
- In a horizontal unifrom electirc field, a small charged disk is gently...
Text Solution
|
- A positively charged disk is rotated clockwise as shown in Fig. The di...
Text Solution
|
- A unifrom solid disk of radius R and mass M is free to rotate on a fri...
Text Solution
|
- A solid unifrom disk of mass m and radius R is pivoted about a horizon...
Text Solution
|
- A uniform solid disk rolling down an incline making angle theta with t...
Text Solution
|
- A solid uniform disk of mass m rolls without slipping down a fixed inc...
Text Solution
|