Similar Questions
Explore conceptually related problems
Recommended Questions
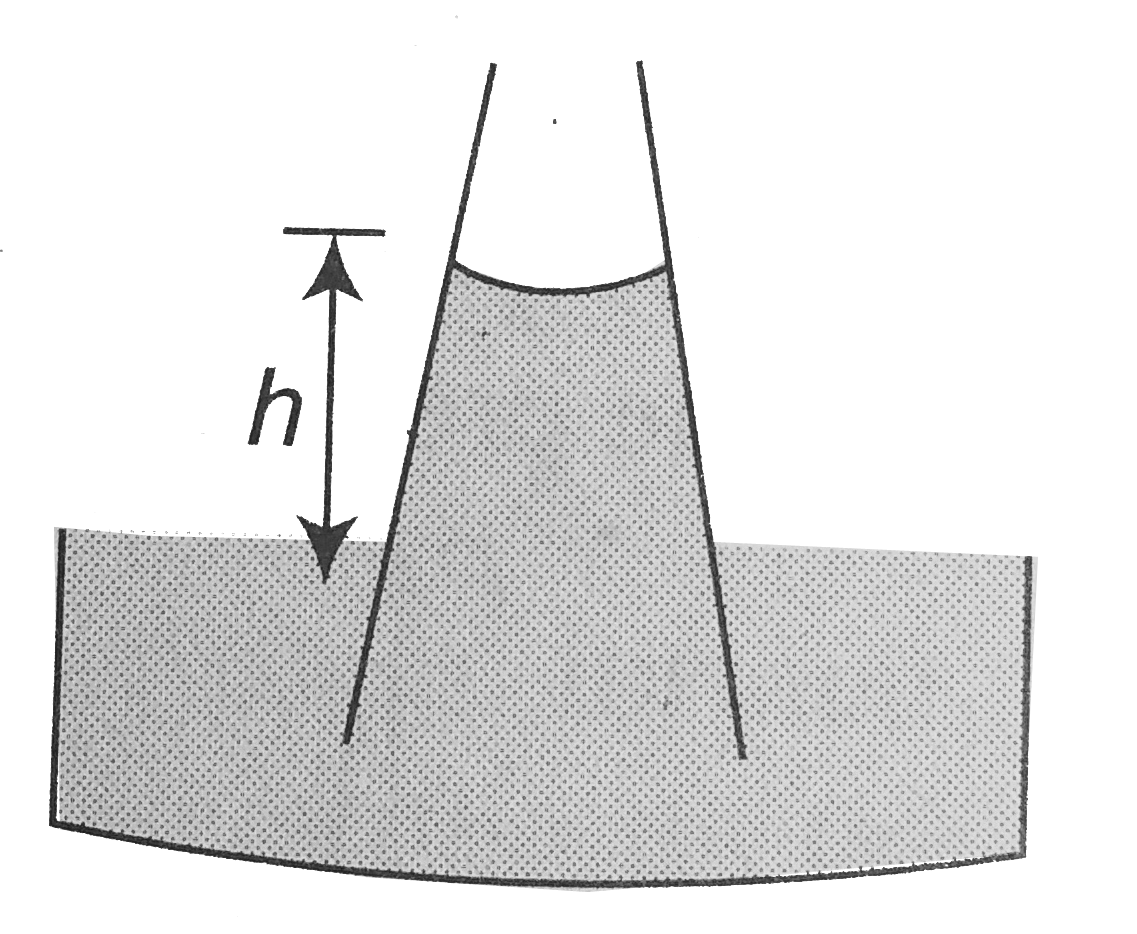
- A capillary of the shape as shown is dipped in a liquid. Contact angle...
Text Solution
|
- When a vertical capillary of length with the sealed upper end was brou...
Text Solution
|
- A capillary of the shape as shown is dipped in a liquid. Contact angle...
Text Solution
|
- A capillary tube with inner cross-section in the form of a square of s...
Text Solution
|
- A capillary tube of radius r is lowered into a liquid of surface tensi...
Text Solution
|
- The height of liquid column in capillary tube is h the radius of capil...
Text Solution
|
- The radius of the bore of a capillary tube is r and the angle of conta...
Text Solution
|
- A liquid of density rho and surface tension sigma rises in a ca...
Text Solution
|
- A capillary of radius 0.15mm is dipped in liquid of density 'rho' = 66...
Text Solution
|