Similar Questions
Explore conceptually related problems
Recommended Questions
- A spaceship is sent to investigate a planet of mass M and radius R. Wh...
Text Solution
|
- A spaceship is sent to investigate a planet of mass M and radius R . W...
Text Solution
|
- A spaceship approaches the Moon (mass = M and radius = R along a parab...
Text Solution
|
- Spacemen Fred's spaceship (which has negligible mass) is in an ellipti...
Text Solution
|
- Two solid spherical planets of equal radii R having masses 4M and 9M t...
Text Solution
|
- A spaceship is moving directly towards a planet at a speed of c/2 . Wh...
Text Solution
|
- M और 16 M द्रव्यमान के दो ग्रह 10a दुरी पर स्थित हैं। उनकी त्रिज्याएँ ...
Text Solution
|
- M द्रव्यमान के ग्रह के चारों ओर m द्रव्यमान का उपग्रह चक्कर लगा रहा है...
Text Solution
|
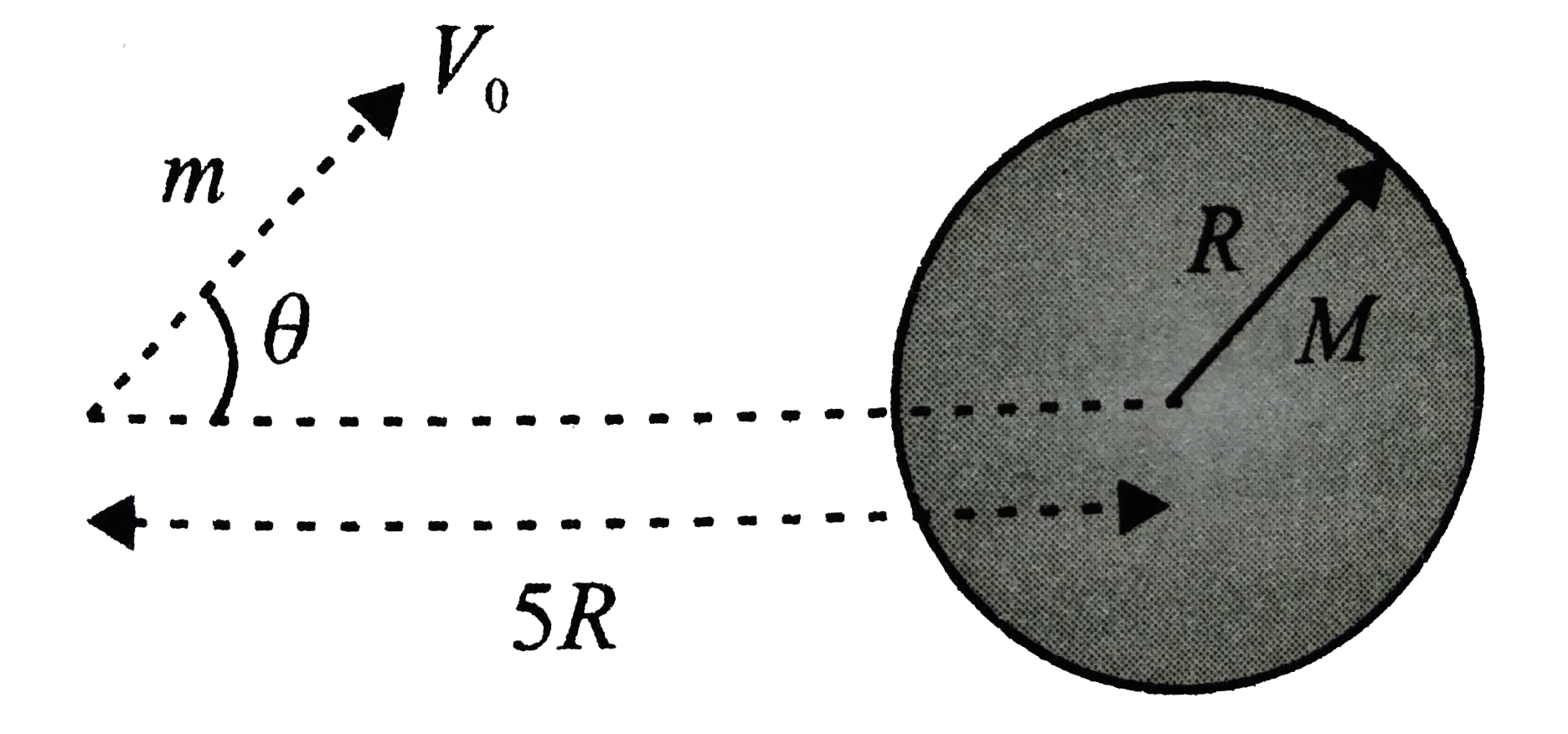
- With what speed v(0) should a body be projected as shown in the figure...
Text Solution
|