Similar Questions
Explore conceptually related problems
Recommended Questions
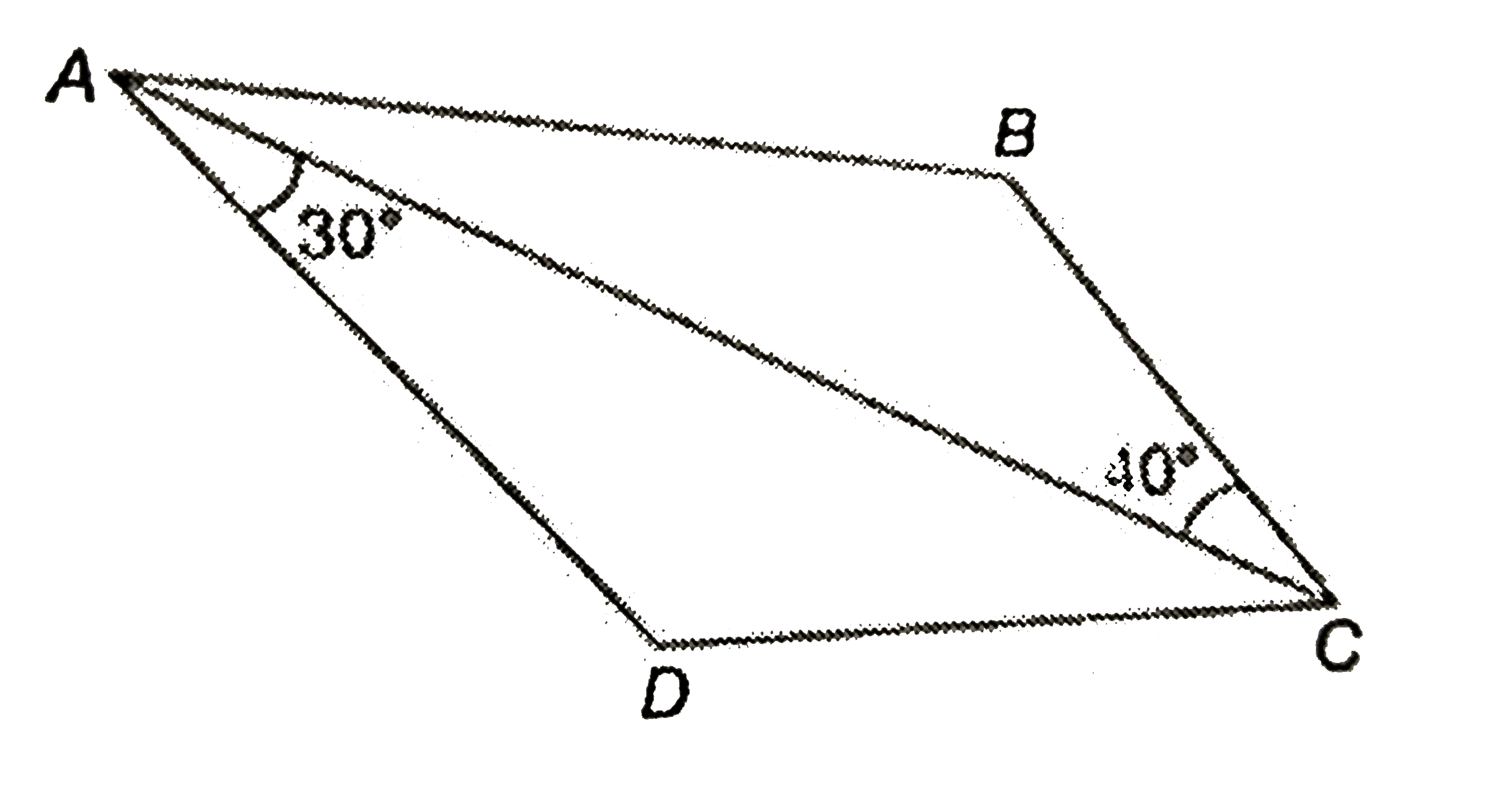
- In the figure, bar(DC)" || "bar(AB). If angleACB=40^(@) and angleCAD=3...
Text Solution
|
- In the figure, bar(DC)" || "bar(AB). If angleACB=40^(@) and angleCAD=3...
Text Solution
|
- In the figure given below, bar(ED)||bar(AB) and bar(EF)||bar(BC) . If ...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- In the figure above (not to scale), overline(AB)botoverline(CD) and AD...
Text Solution
|
- In the given figure, AB is a diameter, O is the center of the circle ...
Text Solution
|
- Draw the bisector of angleAOB=58^(@) ltimg src="https://d10lpgp6xz60...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|