Similar Questions
Explore conceptually related problems
Recommended Questions
- A mass is suspended separately by two different springs in successive ...
Text Solution
|
- A mass is suspended separately by two springs and the time periods in ...
Text Solution
|
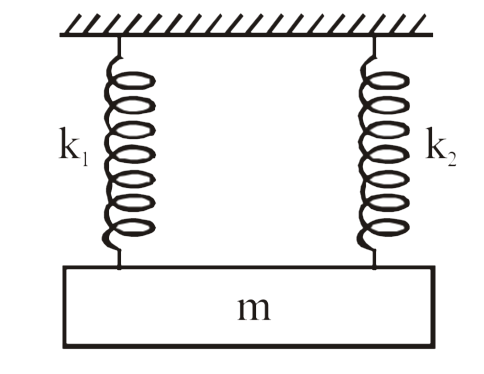
- A mass m is suspended separately by two different springs of spring co...
Text Solution
|
- In an elevator, a spring clock of time period T(s) (mass attached to ...
Text Solution
|
- A mass is suspended separately by two different springs in successive ...
Text Solution
|
- A mass is suspended separately by two springs of spring constants k(1)...
Text Solution
|
- Let T(1) and T(2) be the time periods of two springs A and B when a ma...
Text Solution
|
- Periodic time of oscillation T(1) is obtained when a mass is suspended...
Text Solution
|
- When a block of mass m is suspended separately by two different spring...
Text Solution
|