Text Solution
Verified by Experts
Topper's Solved these Questions
CONIC SECTIONS
NCERT|Exercise EXERCISE 11.4|14 VideosCONIC SECTIONS
NCERT|Exercise EXERCISE 11.2|12 VideosCONIC SECTIONS
NCERT|Exercise EXERCISE 11.1|15 VideosCOMPLEX NUMBERS AND QUADRATIC EQUATIONS
NCERT|Exercise EXERCISE 5.4|6 VideosINTRODUCTION TO THREE DIMENSIONAL GEOMETRY
NCERT|Exercise EXERCISE 12.1|4 Videos
Similar Questions
Explore conceptually related problems
NCERT-CONIC SECTIONS-SOLVED EXAMPLES
- Find the equation of the hyperbola where foci are (0,+-12)and the leng...
Text Solution
|
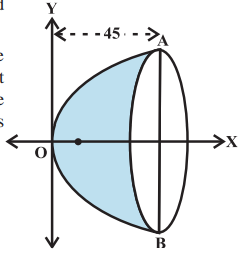
- The focus of a parabolic mirror is at a distance of 5 cm from its ver...
Text Solution
|
- Find the coordinates of the foci and the vertices, the eccentricity, ...
Text Solution
|
- Find the equation of the hyperbola with foci (0,+-3)and vertices (0,+-...
Text Solution
|
- Find the equation of the ellipse, whose length of the major axis is 2...
Text Solution
|
- Find the equation of the ellipse, with major axis along the x-axis an...
Text Solution
|
- Find the coordinates of the foci, the vertices, the lengths of major ...
Text Solution
|
- Find the equation of the ellipse whose vertices are (+-13 ,0)and foci ...
Text Solution
|
- A beam is supported at its ends by supports which are 12 metres apart....
Text Solution
|
- A rod AB of length 15 cm rests in between two coordinate axes in such...
Text Solution
|
- Find an equation of the circle with centre at (0,0) and radius r.
Text Solution
|
- Find the centre and the radius of the circle x^2+y^2+8x+10 y-8=0.
Text Solution
|
- Find the equation of the circle with centre (–3, 2) and radius 4.
Text Solution
|
- Find the coordinates of the focus, axis, the equation of the directri...
Text Solution
|
- Find the equation of the circle which passes through the points (2,-2)...
Text Solution
|
- Find the equation of the parabola with vertex at (0, 0) and focus at ...
Text Solution
|
- Find the equation of the parabola with focus (2, 0) and directrix x=-2...
Text Solution
|
- Find the coordinates of the foci, the vertices, the length of major a...
Text Solution
|
- Find the equation of the parabola with vertex at origin, symmetric wit...
Text Solution
|