Similar Questions
Explore conceptually related problems
Recommended Questions
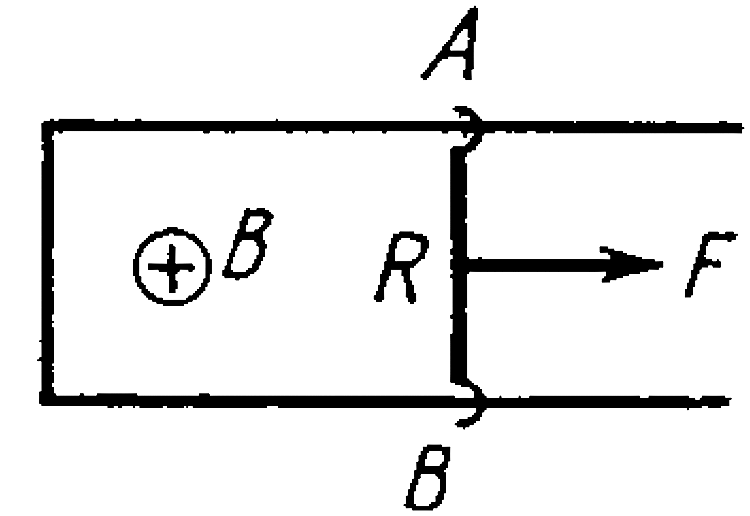
- A connector AB can slide without frictiion along a II-shaped cond...
Text Solution
|
- A rectangular loop with a sliding connector of length l is located in ...
Text Solution
|
- A rectangle loop with a sliding connector of length l=1.0 m is situate...
Text Solution
|
- A long straight wire carrying a current I and a II - shaped conductor ...
Text Solution
|
- A copper connector of mass m slides down two smooth cooper bars, s...
Text Solution
|
- A connector AB can slide without frictiion along a II-shaped cond...
Text Solution
|
- A loop (figure) is formed by two parallel conductores connected by a s...
Text Solution
|
- A conductor of length l and mass m can slide without any friction alon...
Text Solution
|
- A loop is formed by two parallel conductors connected by a solenoid wi...
Text Solution
|