Similar Questions
Explore conceptually related problems
Recommended Questions
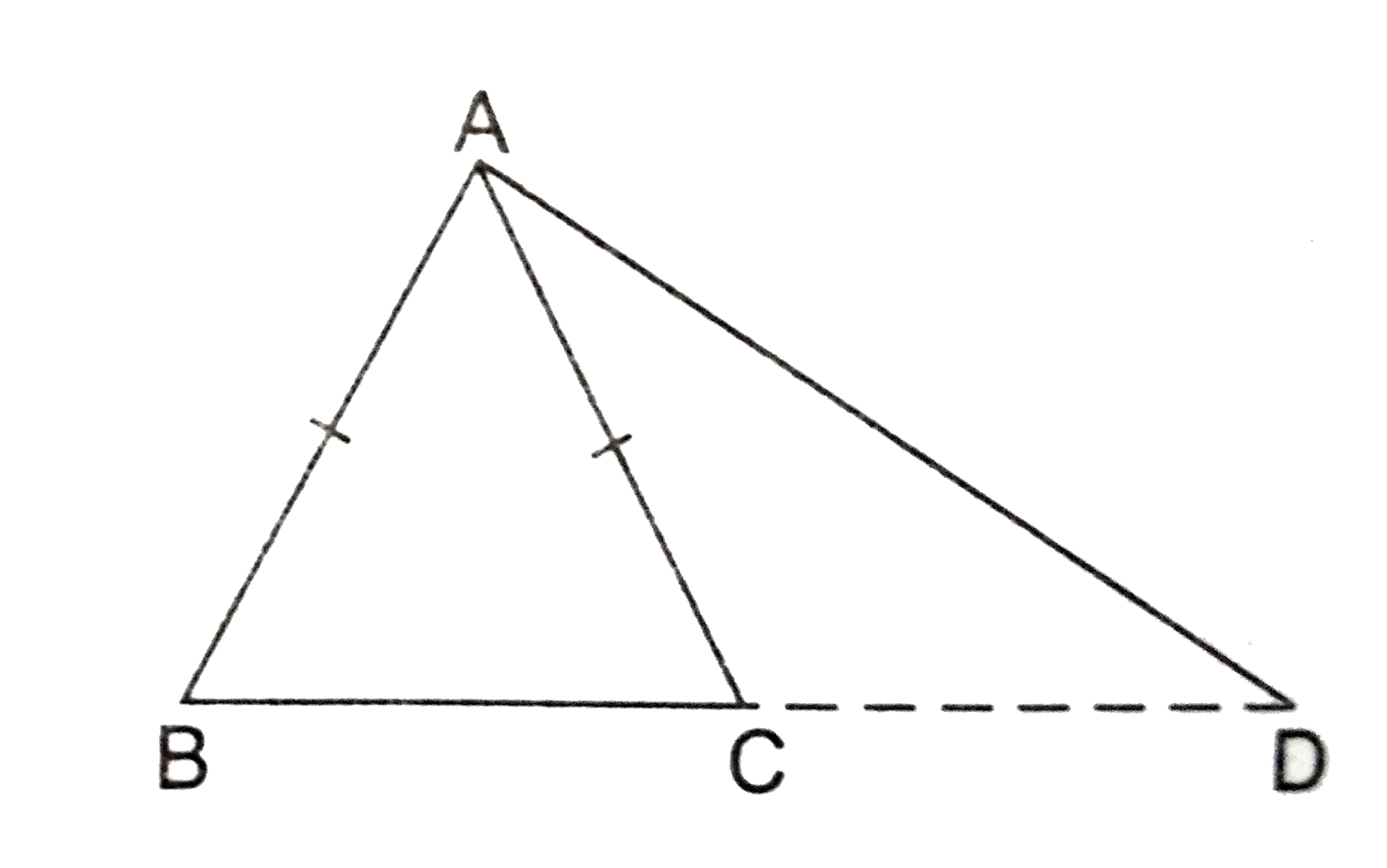
- In Delta ABC, AB= AC. Side BC is produced to D. Prove that (AD^(2)-AC^...
Text Solution
|
- ABC is a triangle in which AB=AC and D is a point on AC such that BC^(...
Text Solution
|
- In the above figure, GH ||IJ and AC || BD, AB and CD are bisectors of ...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- In the figure above (not to scale), overline(AB)botoverline(CD) and AD...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|