Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylinder rod of length 1, thermal conductivity K and area of cross s...
Text Solution
|
- A cylinder rod of length 1, thermal conductivity K and area of cross s...
Text Solution
|
- One end of a thermally insulated rod is kept at a temperature T1 and t...
Text Solution
|
- A rod of length l with thermally insulated lateral surface consists of...
Text Solution
|
- Eleven identical rods are arranged as shown in Fig. Each rod has lengt...
Text Solution
|
- A cylindrical rod of length l, thermal conductivity k and area of cros...
Text Solution
|
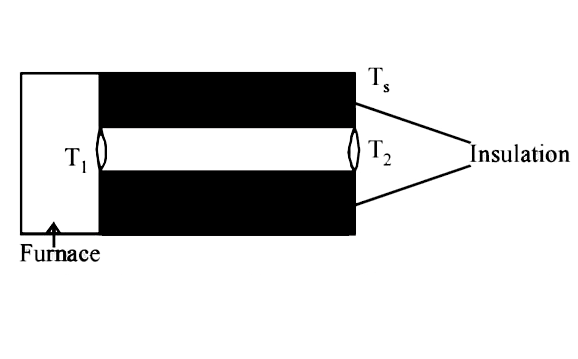
- One end of rod of length L and cross-sectional area A is kept in a fur...
Text Solution
|
- A rod of length l and cross-section area A has a variable thermal cond...
Text Solution
|
- लम्बाई L तथा अनुप्रस्थ - क्षेत्रफल A वाली छड़ का एक सिरा T(1) तापमान व...
Text Solution
|