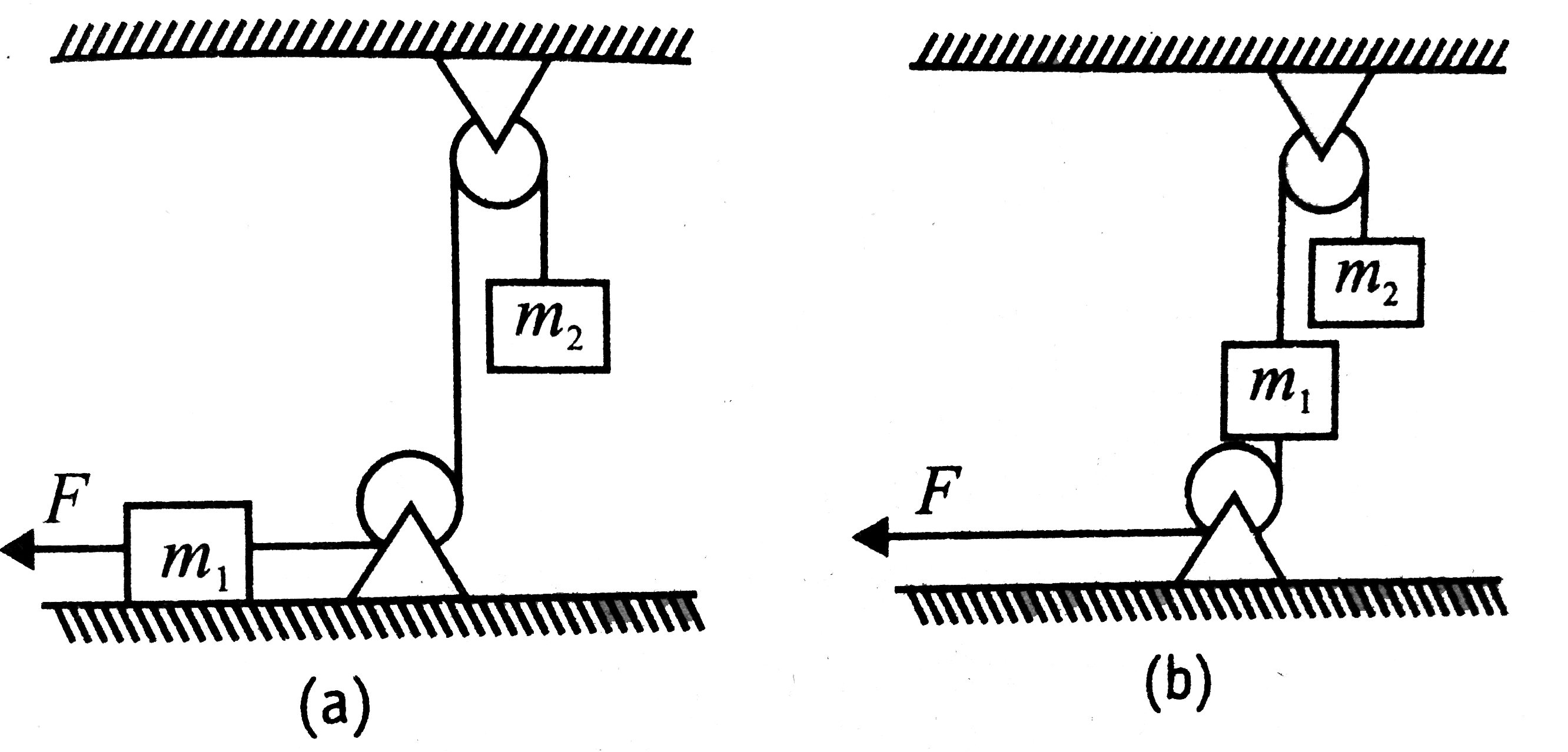
The ratio of tensions in the string connected to the block of mass `m_(2)` in figure, respectively, is (friction is absent everywhere):`[m_(1)=50 kg, m_(2)=80kg` and `F=1000N]`

Find the mass M so that it remains at rest in the abjoining figure. Both the pulley and string are light and friction is absent everywhere. (g = 10 m//s^(2))

Find the mass M so that it remains at rest in the abjoining figure. Both the pulley and string are light and friction is absent everywhere. (g = 10 m//s^(2))

As shown in Fig. three blocks connected together lie on a horizontal frictionless table and pulled to the right with a force F = 50 N. If m_(1)=5kg, m_(2)=10kg and m_(3)=15kg , find the tensions T_(1) and T_(2) .

As in the diagram three blocks connected together lie on a horizontal frictionless table and pulled to the right with a force F=50 N if m_(1)=5kg m_(2)=10 kg and m_(3)=15 kg find the tensions T_(1) and T_(2)

Three blocks are connected as shown in figure on a horizontal frictionless table. If m_(1)=1kg , m_(2)=8kg , m_(3)=27kg and T_(3)=36N , T_(2) will be.

In the arrangement shown in the figure, friction exists only between the two blocks, A and B. The coefficient of static friction mu_(s)=0.6 and coefficient of kinetic friction mu_(k)=0.4 , the masses of the blocks A and B are m_(1)=20 kg and m_(2)=30kg , respectively. Find the acceleration (in ms^(-2) ) of m_(1) , if a force F=150N is applied, as shown in the figure. [Assume that string and pulleys are massless]

A block of mass 'm' is raised by a man of mass m_2 in two different ways as shown ( m_1 = 25kg, m_2 = 50kg)

A block of mass 'm' is raised by a man of mass m_2 in two different ways as shown ( m_1 = 25kg, m_2 = 50kg)

There blocks of masses m_(1),m_(2) and m_(3) are connected by massless strings as shown in figure on a frictionless table. They are pulled with a force T_(3)=50 N. If m_(1)=10 kg, m_(2)=6 kg and m_(3)=2 kg, the tension T_(2) will be