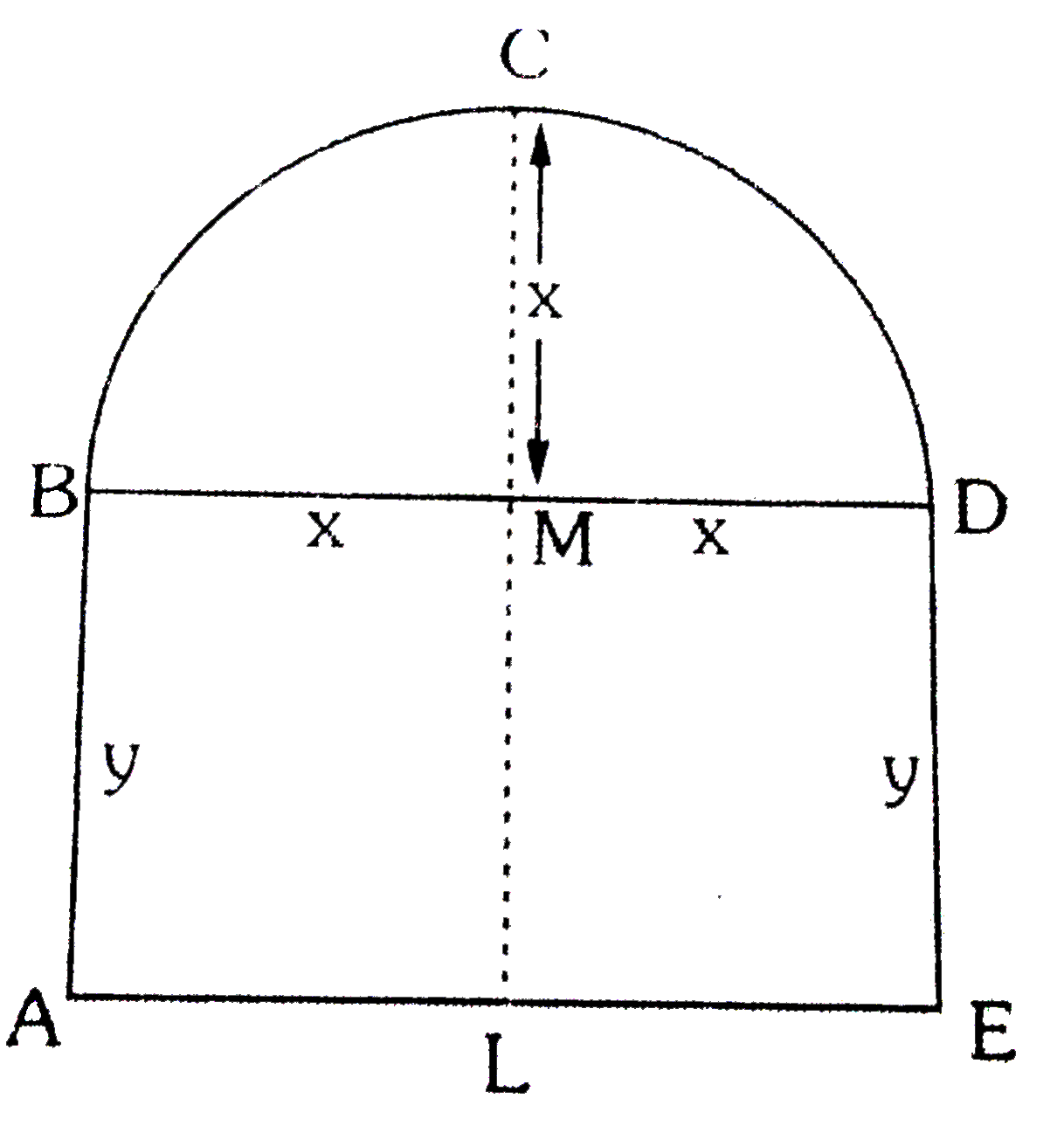लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
उच्चिष्ठ एवं निम्निष्ठ
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 11.1|18 Videosउच्चिष्ठ एवं निम्निष्ठ
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 11.2|14 Videosउच्चिष्ठ एवं निम्निष्ठ
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परीक्षण|19 Videosआव्यूह
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परिक्षण|17 Videosखण्डश: समाकलन
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परीक्षण|28 Videos
BALAJI PUBLICATION-उच्चिष्ठ एवं निम्निष्ठ-विविध उदाहरण
- दर्शाओ कि फलन x^(3) - 3x^(2) + 6x + 3 का मान न उच्चिष्ठ है और न निम...
Text Solution
|
- यदि x = - 1 तथा x = 2 पर फलन y = a log x + bx^(2) + x के चरम मान ह...
Text Solution
|
- एक खिड़की की आकृति एक आयत तथा इस पर बने एक अर्द्धवृत्त की तरह है...
Text Solution
|
- C^(2) वर्ग इकाई धातु से वर्गाकार आधार का एक खुला संदूक बनाना है स...
Text Solution
|
- सिद्ध कीजिये कि सबसे बड़े शंकु का आयतन जो कि त्रिज्या R के गोले ...
Text Solution
|
- सिद्ध कीजिये कि त्रिज्या R के गोले से उच्चिष्ठ आयतन का जो बेलन काट...
Text Solution
|
- यदि एक समलम्ब चतुर्भुज की आधार के अतिरिक्त अन्य तीन भुजायें समान ...
Text Solution
|
- एक फर्म का लागत फलन C = 200 x - 20/3 x^(2) + 2/9 x^(3) द्वारा दिया ...
Text Solution
|
- किसी फर्म का लागत फलन C (x) = 300 x - 10 x^(2) + 1/3 x^(3) द्वारा द...
Text Solution
|
- दो धनात्मक संख्याएँ x तथा y ज्ञात कीजिए जब (x + y) = 60 तथा xy^(3) ...
Text Solution
|
- सिद्ध कीजिए कि दिये गये समकोण त्रिभुज का क्षेत्रफल अधिकतम है यदि ...
Text Solution
|
- सिद्ध कीजिए कि दिये गये क्षेत्रफल वाले आयतों में वर्ग का परिमाप नि...
Text Solution
|
- सिद्ध कीजिए कि एक वृत्त के अंतर्गत स्थित आयतों में वर्ग का क्षेत्र...
Text Solution
|
- सिद्ध कीजिए कि दिये गये आयतन के एक बेलन जो ऊपर से खुला है , का सम्...
Text Solution
|
- सिद्ध कीजिए की अधिकतम आयतन तथा दी गयी तिर्यक ऊँचाई वाले शंकु क...
Text Solution
|
- सिद्ध कीजिए कि दिये गये वक्रपृष्ठ वाले बेलन जो ऊपर से खुला है , क...
Text Solution
|
- एक कार्ड बोर्ड (24 xx 24) सेमी के कोनो से बराबर वर्गों को काटकर तथा ...
Text Solution
|
- सिद्ध कीजिए कि के गोले के अंतर्गत महत्तम आयतन के शंकु के लिए उसक...
Text Solution
|
- सिद्ध कीजिए कि दिये गये आयतन तथा न्यूनतम वक्रपृष्ठ वाले लंबवृत्तीय श...
Text Solution
|
- सिद्ध कीजिए कि महत्तम आयतन के उस लंबवृत्तीय शंकु की ऊँचाई जो r त्रि...
Text Solution
|