विधि`1`: रचना के चरण :
चरण `1` : `AB=7.8` सेमी का एक रेखाखण्ड खींचिये ।
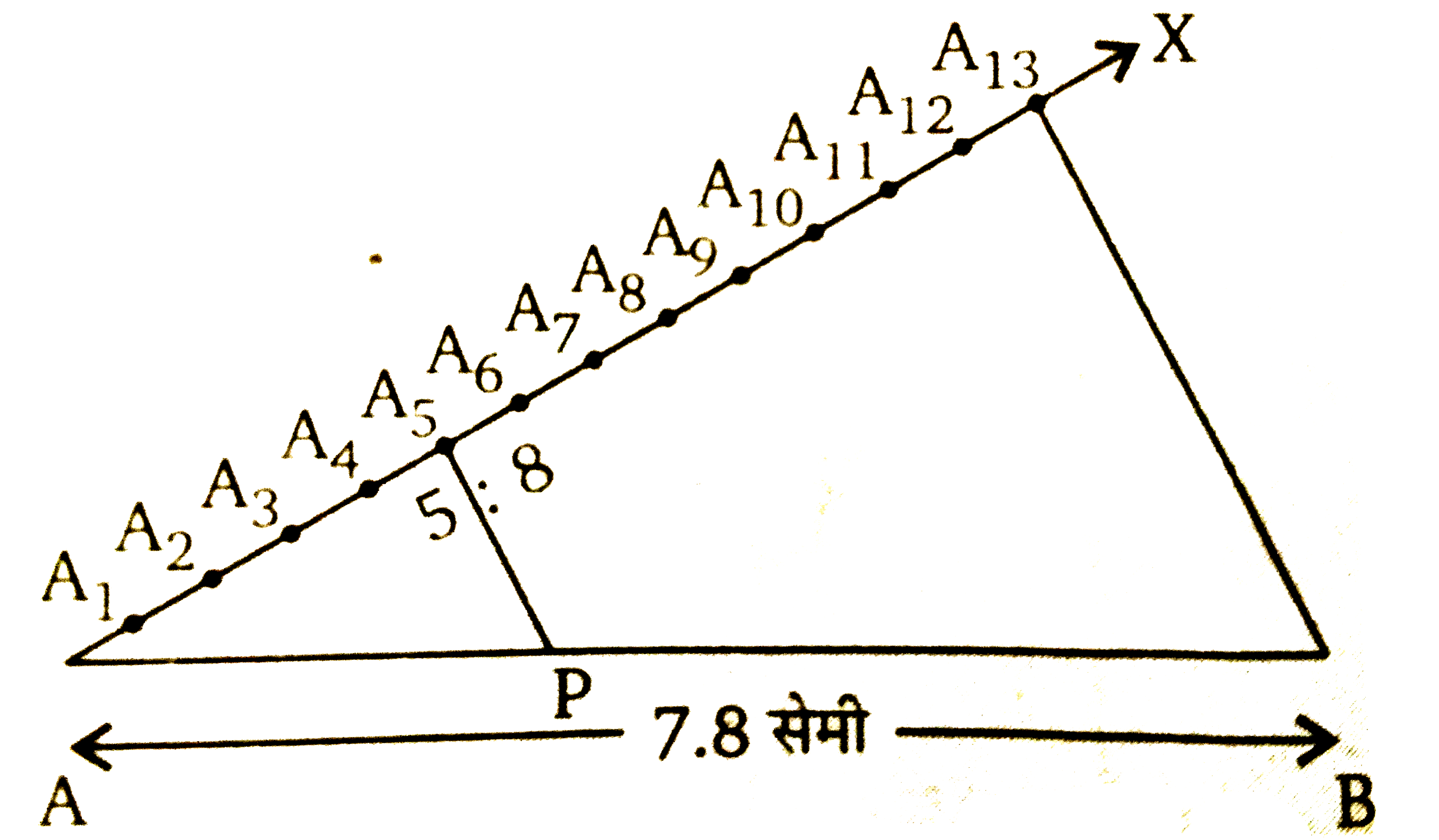
चरण `2` : एक किरण `AX` कोई उपुक्त न्यूनकोण `/_BAX` बनते हुए खींचिये ।
चरण `3` : `AX` दिशा में `(5+8)=13` बिन्दुओ `A_(1),A_(2)....A_(13)` को इस प्रकार चिन्हित कीजिए कि
`"AA"_(1)=A_(1)A_(2)=A_(12)A_(13)`
चरण `4` : `A_(13) B` को मिलाएं।
चरण `5` : `A_(5)` से `A_(5) P||A_(13) B` खीचिए जो `AB` से `P` पर मिलती है। तब `P,AB` पर बिन्दु है जो इसे `5 : 8` के अनुपात में अन्तः विभाजित करता है।
औचित्य :
`A_(5)P||A_(13)Pimplies(AP)/(PB)=("AA"_(5))/(A_(5)A_(13))=(5x)/(8x)=(5)/(8)`
विधि`1`: रचना के चरण :
चरण `1` : `AB=7.8` सेमी का एक रेखाखण्ड खींचिये ।
चरण `2` : `AX` कोई किरण न्यूनकोण `/_BAX` बनते हुए खींचिये ।
चरण `3` : एक किरण के समान्तर खींचे इसके लिए
`/_ABY=/_BAX`
चरण `4` : बिन्दुओ `A_(1),A_(2),...,A_(5)` को `AX` पर और `B_(1),B_(2),....,B_(8)` को `BY` पर इस प्रकार अंकित करे कि
`"AA"_(1)=A_(1)A_(2)=A_(2)A_(3)=A_(3)A_(4)=A_(4)A_(5)="BB"_(1)=B_(1)B_(2)=...=B_(7)B_(8)`
चरण `5` : `A_(5)B_(8)` को मिला दे जो `AB` को `P` पर प्रतिछेद करती है।
