माना AB तथा AC घर्षणरहि दो आनत तल जो क्रमशः `theta_(1)` तथा `theta_(2)` कोण पर झुके है। AB उत्तरोत्तर पथ है तथा AC निम्नोत्तर पथ है।
माना `m_(1)` और `m_(2)` द्रव्यमान के दो पत्थर विरामावस्था से निचे कि और फिसलना आरम्भ करते है।
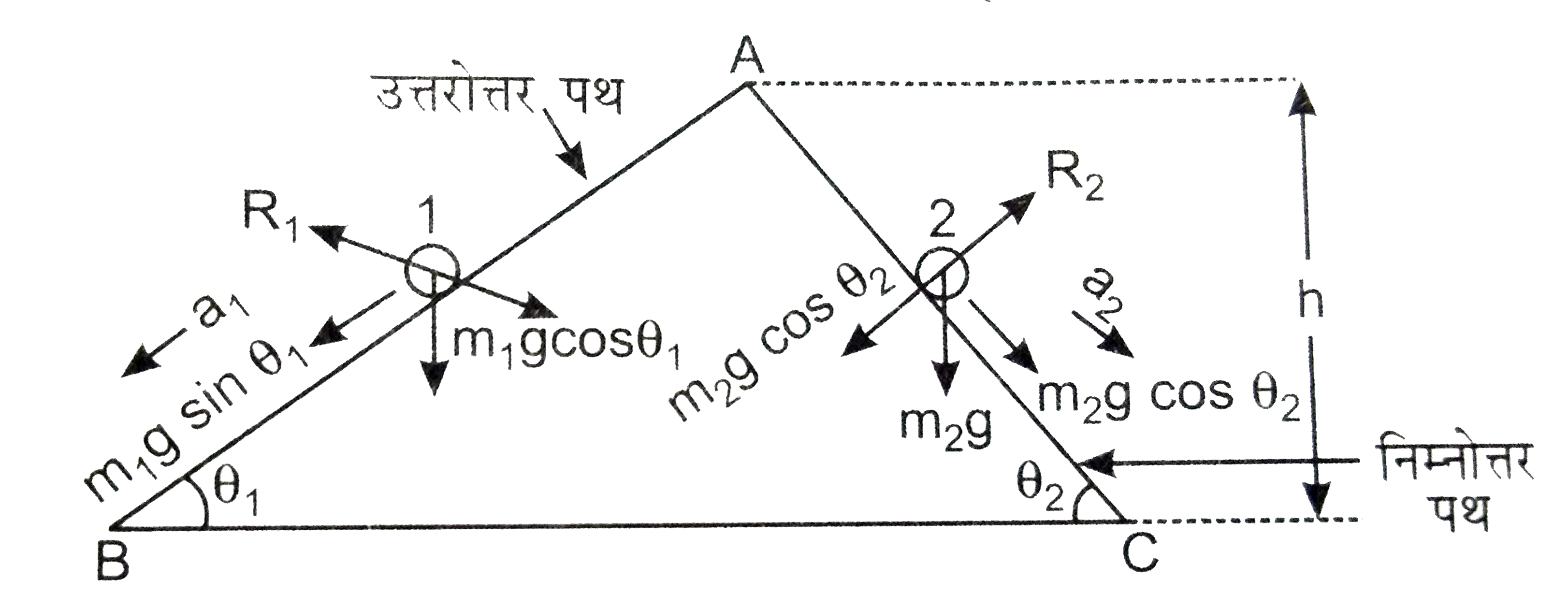
प्रत्येक तल पर A बिन्दु कि ऊँचाई A =10 मीटर विभिन्न बल प्रत्येक पत्थर पर कार्य करते है।
(i) पत्थर का भार (mg) जो ऊर्ध्वार्धरत:, निचे को कार्य करता है अपने दोनों अवयवों शेतृंज घातक `mgcostheta` तथा उर्ध्वाधर घटक `mgsin theta` में विभाजित हो जाता है।
(ii) अभिलम्ब प्रतिक्रिया जो तल के लंबवत है।
माना दो पत्थर के तलो तक पहुँचने में वेग `v_(1)` तथा `v_(2)` है। ऊर्जा संरक्षण के सिद्धांत अनुसार,
स्थितिज ऊर्जा में कमी = गतिज ऊर्जा में वृद्धि
पहले पत्थर के लिए,
`m_(1)gh=1/2m_(1)v_(1)^(2)` या `v_(1)=sqrt(2gh)`
दीसरे पत्थर के लिए,
`m_(2)gh=1/2m_(2)v_(2)^(2)`या `v_(2)=sqrt(2gh)`
अतः `v_(1)=v_(2)=sqrt(2gh)`
दोनों पत्थर समान वेग से निचे पहुँचेगे। पत्थरो के भरो में दोनों अवयव में प्रदर्शित किये गये है। यदि `a_(1)` तथा `a_(2)` दोनों पत्थरो के त्वरण हो, तो उनके भार के क्षैतिज घटक क्रमशः `m_(1)g costheta_(1)` तथा `m_(2)g costheta_(2)` होंगे तथा भार के यह क्षैतिज घातक अभिलम्ब प्रतिक्रिया `R_(1)` तथा `R_(2)`के द्वारा सन्तुलित रहते है।
पत्थरो पर लगे कुल बल `m_(1)gsintheta_(1)` तथा `m_(2)g sin theta_(2)` है जो निचे कि और कार्य करते है तथा या बल इन बालो के कारन पत्थर गति करते है।
`m_(1)a_(1)=m_(1)g sintheta_(1)`
या `a_(1)=g sin theta_(1)`
इसी प्रकार, `m_(2)a_(2)=m_(2)g sintheta_(2)`
या `a_(2)=gsin theta_(2)` और `theta_(2)=30^(@)`
तथा `theta_(1)=60^(@)`
`thereforea_(1)=gsin30^(@)` =gxx1/2=g/2`
तथा `a_(2)gta_(1)` या `(a_(2))/(a_(1))gt1`
गति की समीकरण से, `v=u+at` अथवा `v=0+at`
`(u=0` क्योकि दोनों पत्थर विरामावस्था में है)
या `v=at`
या `a=v/t`
चूँकि दोनों पत्थर समान वेग से तल पर पहुँचते है इसलिये वेग नियत है।
`thereforeaprop1/t` या `tprop1/a`
`therefore(t_(1))/(t_(2))=(a_(2))/(a_(1))`
लेकिन, `(a_(2))/(a_(1))gt1`
`therefore(t_(1))/(t_(2))gt1`
या `t_(1)gtt_(2)`
अतः दूसरे पत्थर से तल पर पहुँचने में कम समय लेगा।
