Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A light spring of spring constant k is kept compressed between two blo...
Text Solution
|
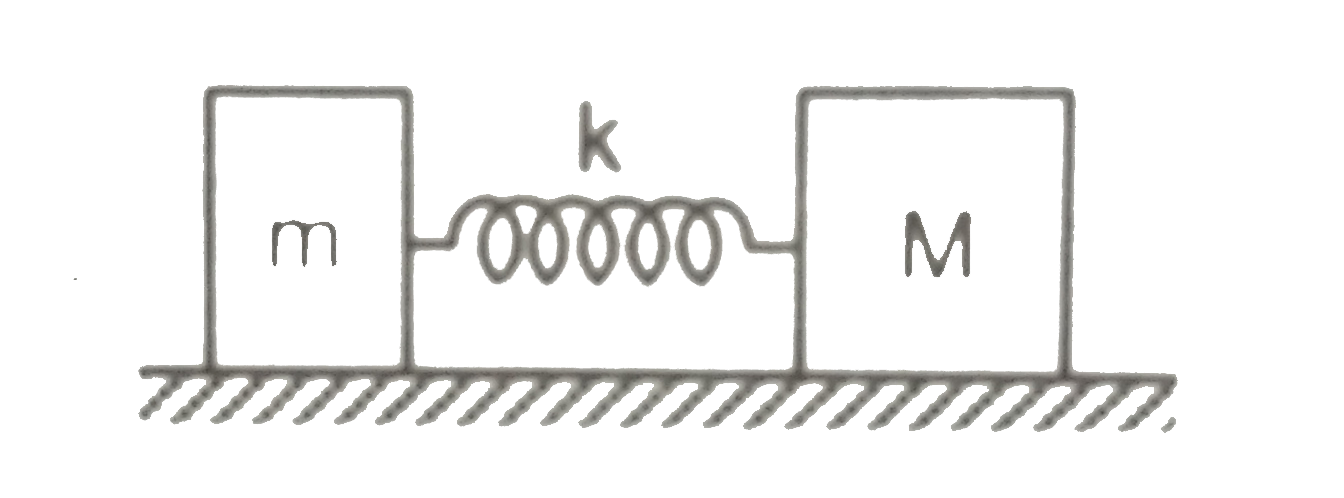
- A block of mass m is connect to another block of mass M by a massless ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- A block of mass m is pushed up against a spring, compressing it a dist...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A block of mass m is placed on a smooth block of mass M = m with the h...
Text Solution
|
- चित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके ए...
Text Solution
|
- A block of mass m is initially moving to the right on a horizontal fri...
Text Solution
|