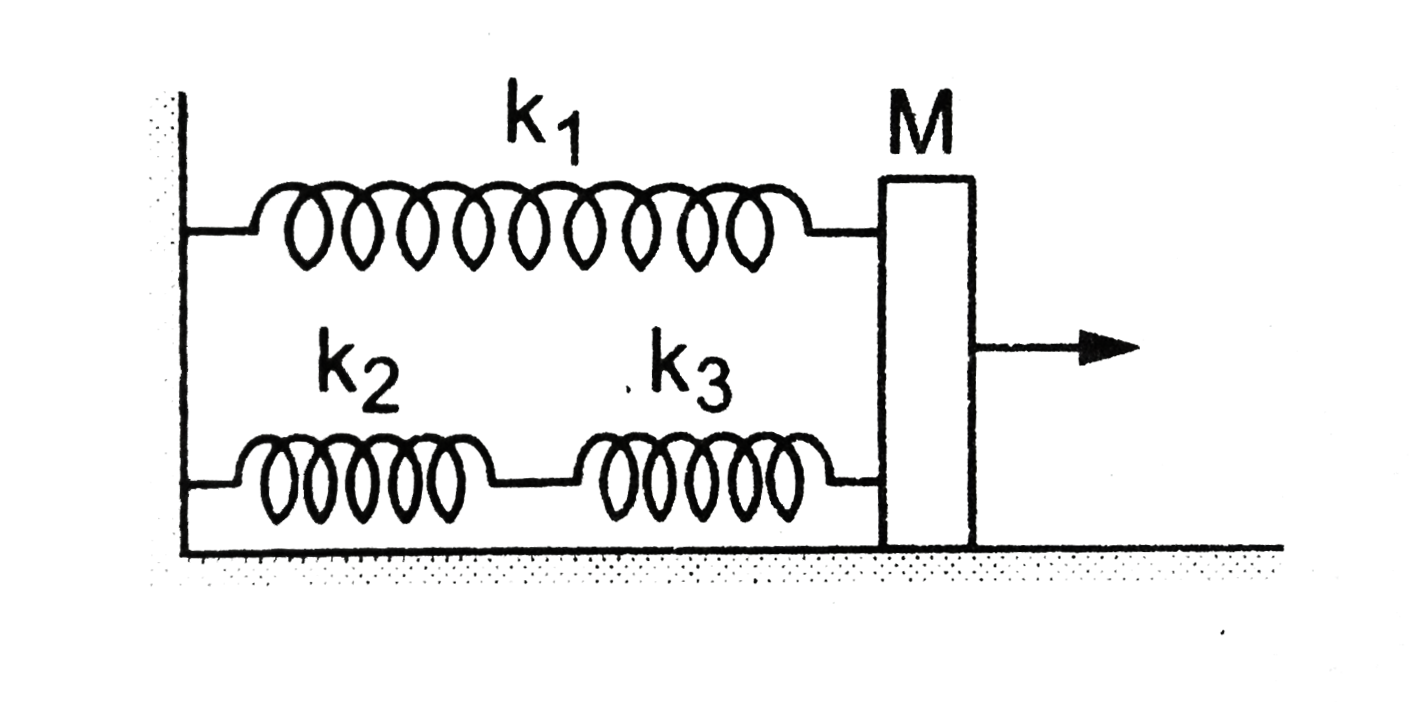Text Solution
Verified by Experts
The correct Answer is:
HC VERMA-SIMPLE HARMONIC MOTION-Exercises
- A particle of mass m is asttached to three springs A,B and C of equla ...
Text Solution
|
- Repeat the previous exercise if the angle between each pair of springs...
Text Solution
|
- The springs shown in the figure are all unstretched in the beginning w...
Text Solution
|
- Find the elastic potential energy stored in each spring shown in figu...
Text Solution
|
- The string ,the spring and the pulley shown in figure are light. Find ...
Text Solution
|
- Solve the previous problem if the pulley has a moment of inertia I abo...
Text Solution
|
- Consider the situastion shown in figure. Show that if that blocks are ...
Text Solution
|
- A rectangular plate of sides a and b is suspended fropm a ceilling by ...
Text Solution
|
- A 1kg block is eecuting simpe hrmonic motion of ampliltude 0.1 m m on ...
Text Solution
|
- The left block in figure moves at a speed v towards the right block pl...
Text Solution
|
- Find the time period of the motion of the particle shown in figure. Ne...
Text Solution
|
- All the surfaces shown in figure are frictionless. The mass of the car...
Text Solution
|
- A uniform table of mas M stays horizontally and symmetrically on two w...
Text Solution
|
- Find the length of seconds pendulum at a place where g = pi^(2) m//s^(...
Text Solution
|
- The angle made by the string of a simple pendulum with the vertical de...
Text Solution
|
- The pendulum of certain clock has time period 2.04 s. How fast or slow...
Text Solution
|
- A pendulum clock giving correct time at a place where g=9.800 ms^-2 is...
Text Solution
|
- A simple pendulum is constructed by hanging a heavy ball by a 5.0 long...
Text Solution
|
- The maximum tension in the string of an oscillating pendulum is double...
Text Solution
|
- A small block oscillates back and forth on as smooth concave surface o...
Text Solution
|