Home
Class 12
MATHS
If the vectors vec(AB)=3hati+4hatk and v...

If the vectors `vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk` are the sides of a triangle ABC, then the length of the median through A is (A) `sqrt(33)` (B) `sqrt(45)` (C) `sqrt(18)` (D) `sqrt(720`

A

`sqrt(18)`

B

`sqrt(72)`

C

`sqrt(33)`

D

`sqrt(288)`

Text Solution

Verified by Experts

The correct Answer is:
C
Position vector of
`AD=((3+5)hati+(0-2)hatj+(4+4)hatk)/(2)`
`(because" D is mid point of BC")`

`=4hati-hatj+4hatk`
`:.|AD|=sqrt((4)^(2)+(-1)^(2)+4^(2))`
`=sqrt(16+1+16)=sqrt(33)`
Promotional Banner

Topper's Solved these Questions

  • PRACTICE SET 18

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PAPER 2 (MATHEMATICS)|50 Videos

  • PRACTICE SET 20

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PAPER 2 (Mathematics)|49 Videos

Similar Questions

Explore conceptually related problems

If the vectors vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk are the sides of a triangle ABC, then the length of the median through A is (A) sqrt(18) (B) sqrt(72) (C) sqrt(33) (D) sqrt(45)

The vectors vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk are the sides of a triangle ABC. The length of the median through A is (A) sqrt(72) (B) sqrt(33) (C) sqrt(2880 (D) sqrt(18)

The vector vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk are sides of a triangle ABC. The length of the median through A is (A) sqrt(18) (B) sqrt(72) (C) sqrt(33) (D) sqrt(288)

If the vectors bar A B=3 hat i+4 hat k and bar A C=5 hat i-2 hat j+4 hat k are the sides of a triangle ABC, then the length of the median through A is (1) sqrt(72) (2) sqrt(33) (3) sqrt(45) (4) sqrt(18)

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 19-Paper 2 (Mathematics)
  1. int sec^(8//9)x cosec^(10//9)x dx is equal to

    Text Solution

    |

  2. Switching function of the network is

    Text Solution

    |

  3. Find the equation of the plane containing the lines (x-5)/4=(y-7)/4...

    Text Solution

    |

  4. If bar a,bar b,bar c are non coplanar vectors and lambda is a real nu...

    Text Solution

    |

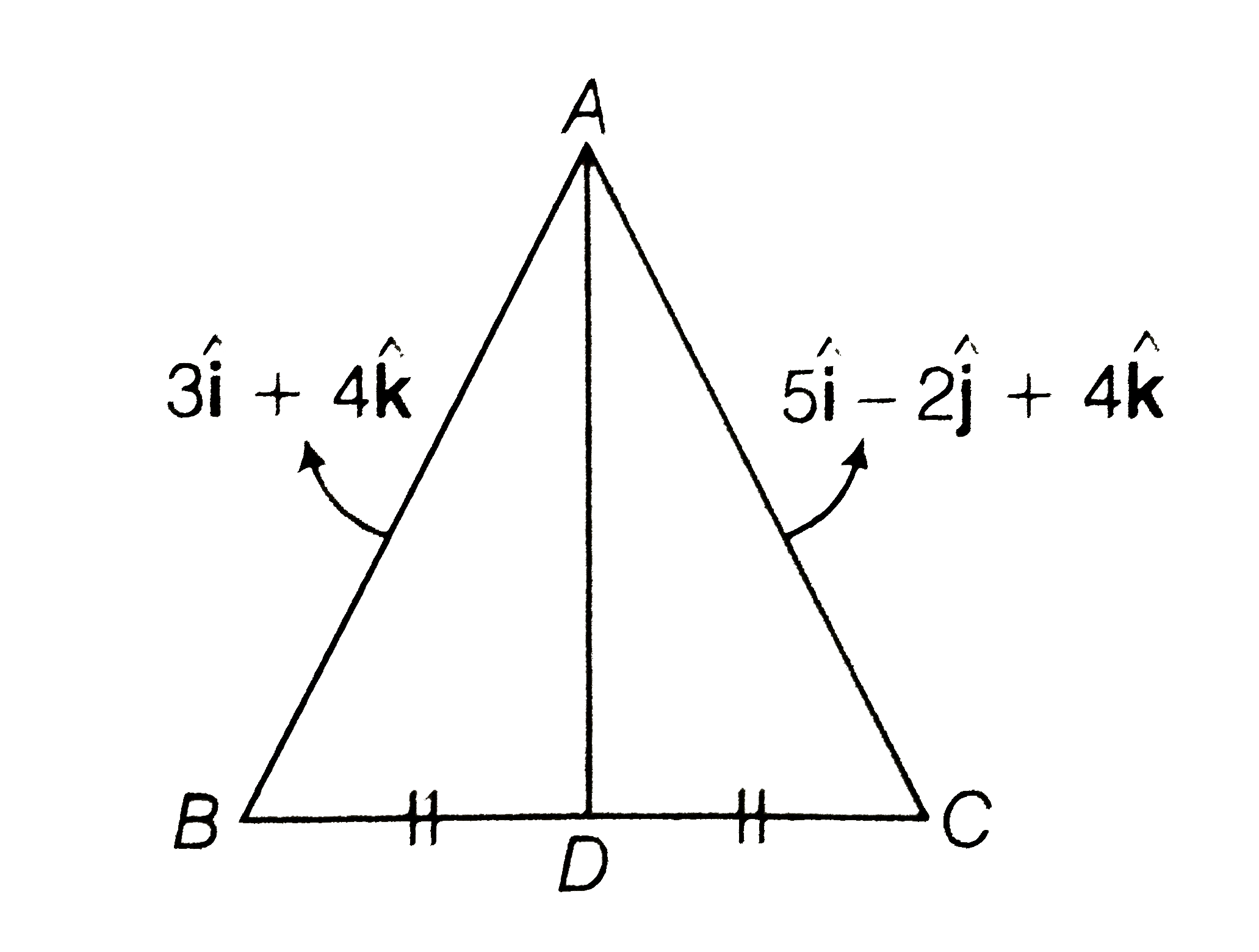
  5. If the vectors vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk are t...

    Text Solution

    |

  6. "I f"int(dx)/(cos^3xsqrt(sin2x))=a(tan^2x+b)sqrt(tanx)+c

    Text Solution

    |

  7. Area bounded by the curve y=sin^(2)x and lines x=(pi)/(2),x=pi and X-a...

    Text Solution

    |

  8. If p and q are two statements, then (p rArr q) iff (~q rArr ~ p) is

    Text Solution

    |

  9. Inequation y-x le 0 represents

    Text Solution

    |

  10. The 5th term of the series (10)/(9),(1)/(3)sqrt((20)/(3)),(2)/(3),… is

    Text Solution

    |

  11. Let (x,y) be any point on the parabola y^2 = 4x. Let P be the point t...

    Text Solution

    |

  12. Equation of the ellipse whose foci are (2, 2) and (4, 2) and the major...

    Text Solution

    |

  13. (sin5theta+sin3theta)/(cos5theta+cos3theta) is equal to

    Text Solution

    |

  14. For the two circles x^2+y^2=16 and x^2+y^2-2y=0, there is/are

    Text Solution

    |

  15. Consider the inequalities x(1)+x(2)le3,2x(1)+5x(2)ge10x(1),x(2)ge0 whi...

    Text Solution

    |

  16. Suppose the cubic x^(3)-px+q has three distinct real roots, where pgt0...

    Text Solution

    |

  17. If f(x+y)=f(x)f(y) for all real x and y, f(6)=3 and f'(0)=10, then f'(...

    Text Solution

    |

  18. A ladder 10 m long rests against a vertical wall with the lower end on...

    Text Solution

    |

  19. If ax^(2)+bx+4 attains its minimum value -1 at x = 1, then the values ...

    Text Solution

    |

  20. The equation of the tangent to the curve y=(2x-1)e^(2(1-x)) at the p...

    Text Solution

    |