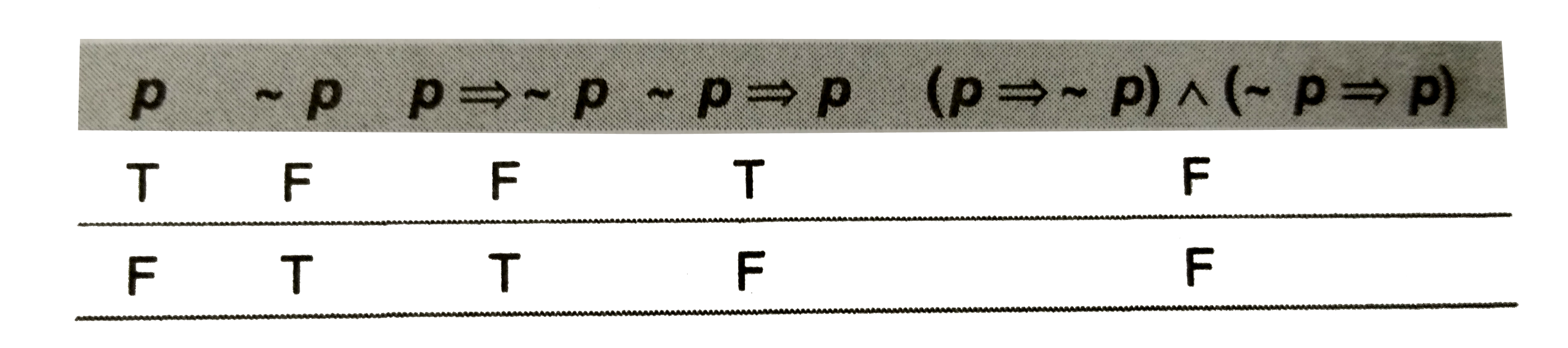A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MATHEMATICAL LOGIC
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))|26 VideosLinear Programming
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|13 VideosMATRICES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|18 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-MATHEMATICAL LOGIC -MHT CET CORNER
- Which of the following quantified statement is true?
Text Solution
|
- Symbolic form of the given switching circuit is equivalent to
Text Solution
|
- The statement (p -> ~p) ^^ (~p -> p) is
Text Solution
|
- The inverse of the statement (p ^^ ~ q) -> r is
Text Solution
|
- If x and y have different truth values, then x ^^ (x vv y) is equivale...
Text Solution
|
- For the circuit shown below, the Boolean polynomial is
Text Solution
|
- Dual of (x vv y) ^^ (x' vv 1) is
Text Solution
|
- If p,q,r are single proposition with truth values T, F, F, then the tr...
Text Solution
|
- The output of the following circuit is
Text Solution
|
- The proposition (~p)vv(p^~q) is equivalent to
Text Solution
|
- ~(~p to q) is equivalent to
Text Solution
|
- Simplify the following circuit and it is equivalent to.
Text Solution
|
- Simplify (p vv q) ^^ (p vv ~q).
Text Solution
|
- Negation of the conditional ''If it rains, I shall go to school'' is
Text Solution
|
- The dual of the statement [p vv(~q)]^^(~p) is
Text Solution
|
- Which of the following statement has the truth value F ?
Text Solution
|
- The negation of the statement ''He is rich and happy'' is given by
Text Solution
|
- ~(p harr q) is a
Text Solution
|
- ~[(p ^^ q)to(~p vv q)] is a
Text Solution
|
- (p ^^ ~q) ^^ (~p ^^ q) is a
Text Solution
|