Home
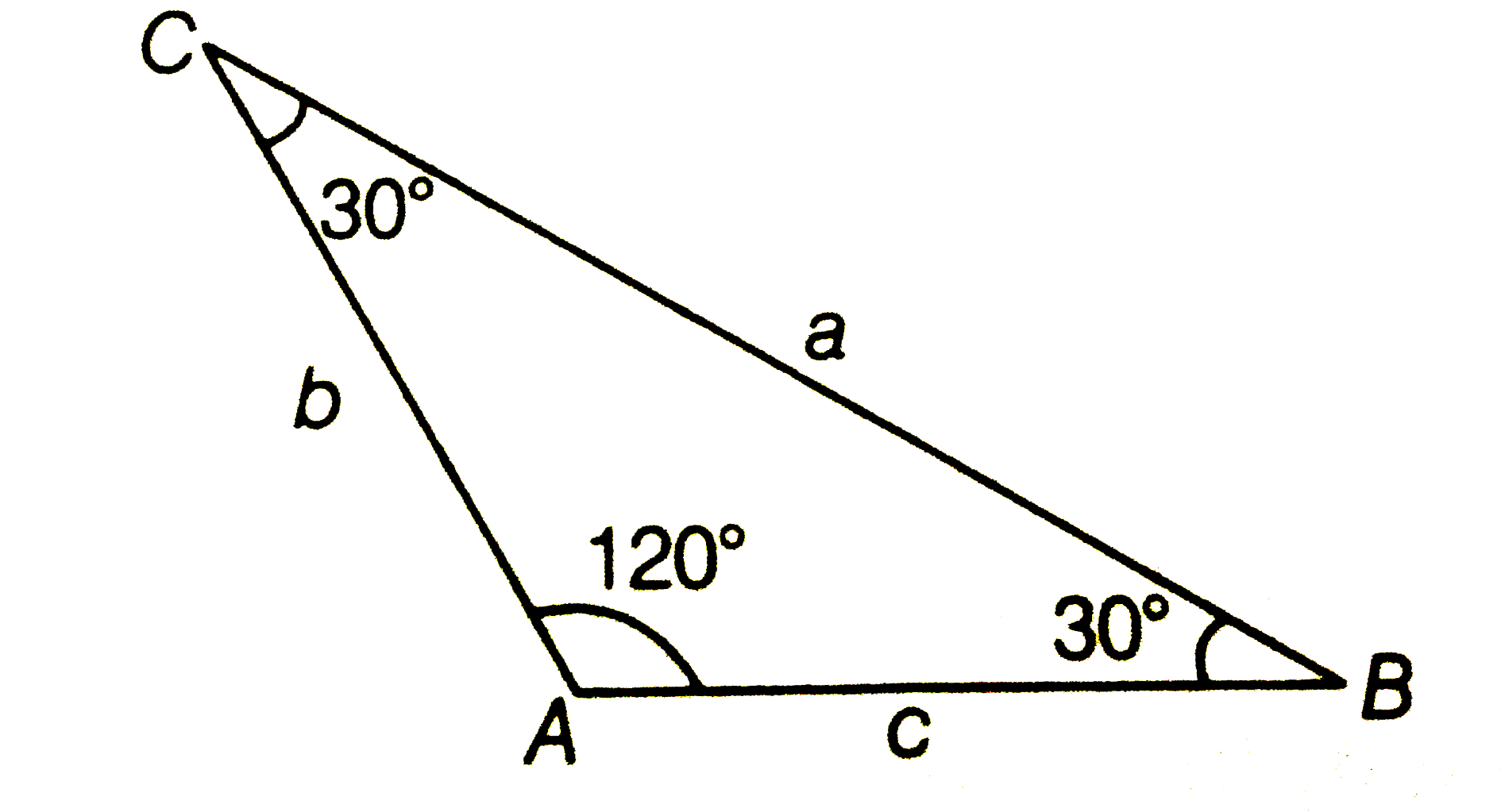
Class 12
MATHS
If the angles of a triangle are in the r...

If the angles of a triangle are in the ratio `4:1:1,` then the ratio of the longest side to the perimeter is

A

`sqrt(3):(2+sqrt(3))`

B

`1 : 6`

C

`1:(2+sqrt(3))`

D

`2 : 3`

Text Solution

Verified by Experts

The correct Answer is:
A
Here , ratio of angles are `4 : 1 : 1`.
`rArr4x+x+x=180^(@)`
`rArrx=30^(@)`
`thereforeangleA=120^(@),angleB=angleC=30^(@)`

Thus ,the ratio of longest side to the perimeter `=(a)/(a+b+c)` Let b = c =x
`thereforea^(2)=b^(2)+c^(2)-2bc cosA`
`rArra^(2)=2x^(2)-2x^(2)cosA=2x^(2)(1-cosA)`
`rArra^(2)=4x^(2)"sin"^(2)(A)/(2)`
`rArra=2x"sin"(A)/(2)`
`rArra=2xsin60^(@)=sqrt(3)x`
Thus ,required ratio is
`(a)/(a+b+c)=(sqrt(3)x)/(x+x+sqrt(3)x)=(sqrt(3))/(2+sqrt(3))`
Promotional Banner

Similar Questions

Explore conceptually related problems

If the angles of the triangle are in the ratio 4:1:1 , then the ratio of the longest side to the perimeter is

The angles of a triangle are in the ratio 4:1:1 . Then the ratio of the largest side to the perimeter is

If the angles of a triangle are in the ratio 7:2:1, then prove that the ratio of smallest side to the largest side is sqrt(5)-1:sqrt(5)+1

If the angles of a triangle are in the ratio 1:4:7 , then the value of the largest angle is :

If the angles are in the ratio 1:1:1 , then the ratio of their sides is

If the angles of a triangle are in the ratio 3:4:5,then the sides are in the ratio