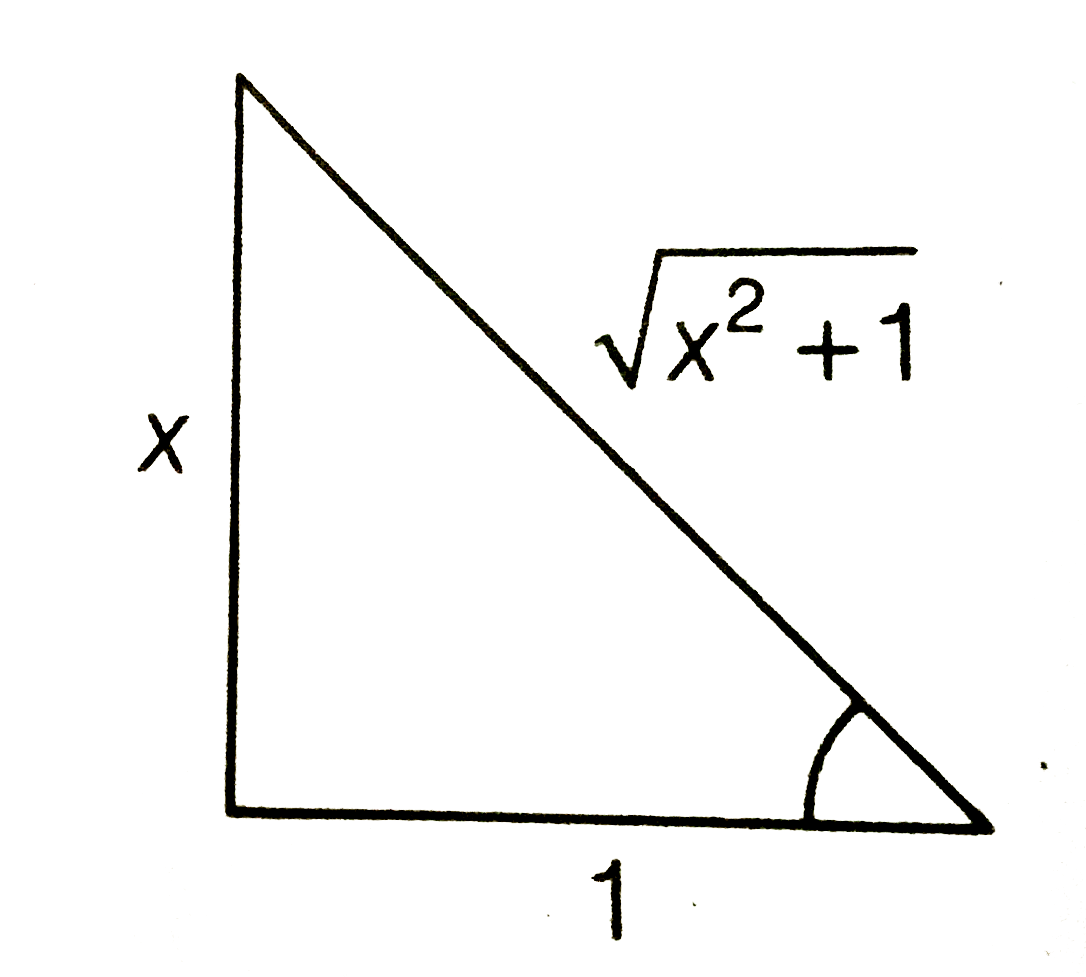
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If"sin"{cot^(-1)(x+1)}="cos"(tan^(-1)x), then find xdot
Text Solution
|
- Evaluate: sin(cot^(-1)x) (ii) cos(tan^(-1)x)
Text Solution
|
- Find the value of sin[cot^(-1){tan(cos^(-1)x)}]
Text Solution
|
- If A=sin[cot^(-1){cos(tan^(-1)x)}], then
Text Solution
|
- If sin[cot^(-1)(1+x)]=cos(tan^(-1)x) Then x =
Text Solution
|
- If sin{cot^(-1)(1+x)}=cos(tan^(-1)x) Then x =
Text Solution
|
- If sin (cot^(-1)(1-x))=cos(tan^(-1)(-x)) , then x is
Text Solution
|
- Find the range of f(x)=sin^(-1)x+tan^(-1)x+cos^(-1)xdot
Text Solution
|
- Find the range of f(x)=sin^(-1)x+tan^(-1)x+cos^(-1)xdot
Text Solution
|