A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MISCELLANEOUS PROBLEMS|80 VideosAPPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 VideosAPPLICATIONS OF DEFINITE INTEGRALS
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 VideosBINOMIAL DISTRIBUTION
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DERIVATIVES-MHT CET CORNER
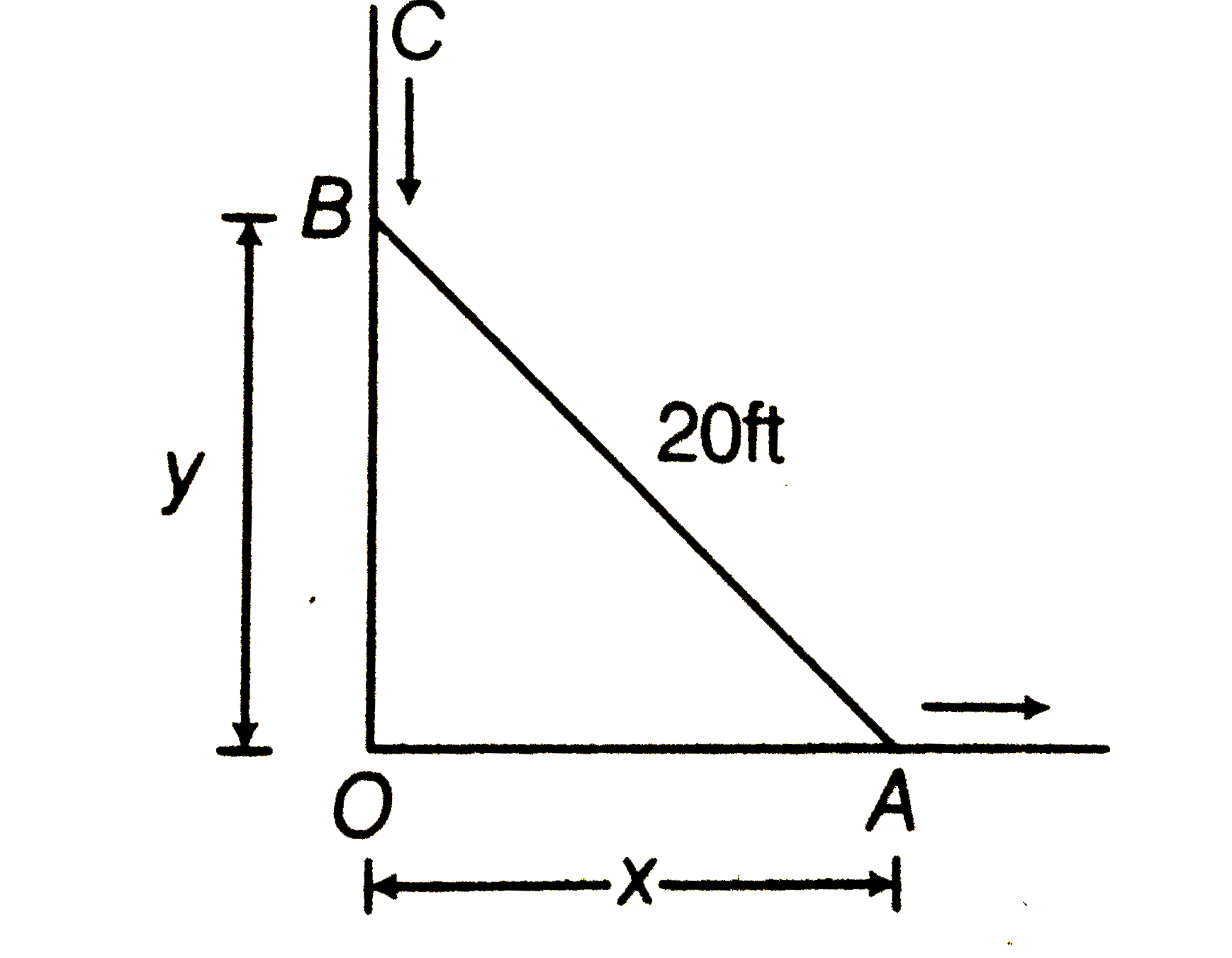
- A ladder 20 ft long has one end on the ground and the other end in con...
Text Solution
|
- If the Rolle's theorem for f(x)=e^(x)(sin x-cosx) is verified on [(pi)...
Text Solution
|
- The approximate value of f(x)=x^(3)+5x^(2)-7x+9 at x=1.1 is
Text Solution
|
- एक कण वक्र 6y= x^3+ 2 के अनुगत गति कर रहा है वक्र पर उन बिंदुओं को ज...
Text Solution
|
- All points on the curve y^(2)=4a(x+a" sin"(x)/(a)) at which the tangen...
Text Solution
|
- The length of normal at any point to the curve, y=c cosh(x/c) is
Text Solution
|
- The height of right circular cylinder of maximum volume in a sphere of...
Text Solution
|
- x,के सभी वास्तविक मानों के लिए (1-x+x^2)/(1+x+x^2) का न्यूनतम मान है ...
Text Solution
|
- If x+y=k is normal to y^2=12 x , then k is 3 (b) 9 (c) -9 (d) -3
Text Solution
|
- A particle moves along a straight line according to the law s=16-2t+3t...
Text Solution
|
- The equation of the tangent at (2,3) on the curve y^2=a x^3+b is y=4x-...
Text Solution
|
- The equation of motion of a particle moving along a straight line is s...
Text Solution
|
- The equation of the tangent to the curve y=4xe^(x) at (-1,(-4)/e) is
Text Solution
|
- The abscissa of the points, where the tangent to curve y=x^(3)-3x^(2)-...
Text Solution
|
- The point of the curve y^(2)=2(x-3) at which the normal is parallel to...
Text Solution
|
- Maximum area of a reactangle which can be inscribed in a circle of a...
Text Solution
|
- If the function f(x)=2x^3-9a x^2+12 x^2x+1,w h e r ea >0, attains its ...
Text Solution
|
- If f(x)= kx-sin x is monotonically increasing then
Text Solution
|
- If a particle moves such that the displacement is proportional to the ...
Text Solution
|
- f(x)=tan^(-1)(sinx+cosx), x gt0 is always and increasing function on t...
Text Solution
|
- A ladder 10 m long rests against a vertical wall with the lower end on...
Text Solution
|