A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 VideosAPPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 VideosAPPLICATIONS OF DEFINITE INTEGRALS
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 VideosBINOMIAL DISTRIBUTION
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DERIVATIVES-MISCELLANEOUS PROBLEMS
- If the distance s covered by a particle in time t is proportional to t...
Text Solution
|
- OB and OC are two roads enclosing an angle of 120^(@). X and Y start a...
Text Solution
|
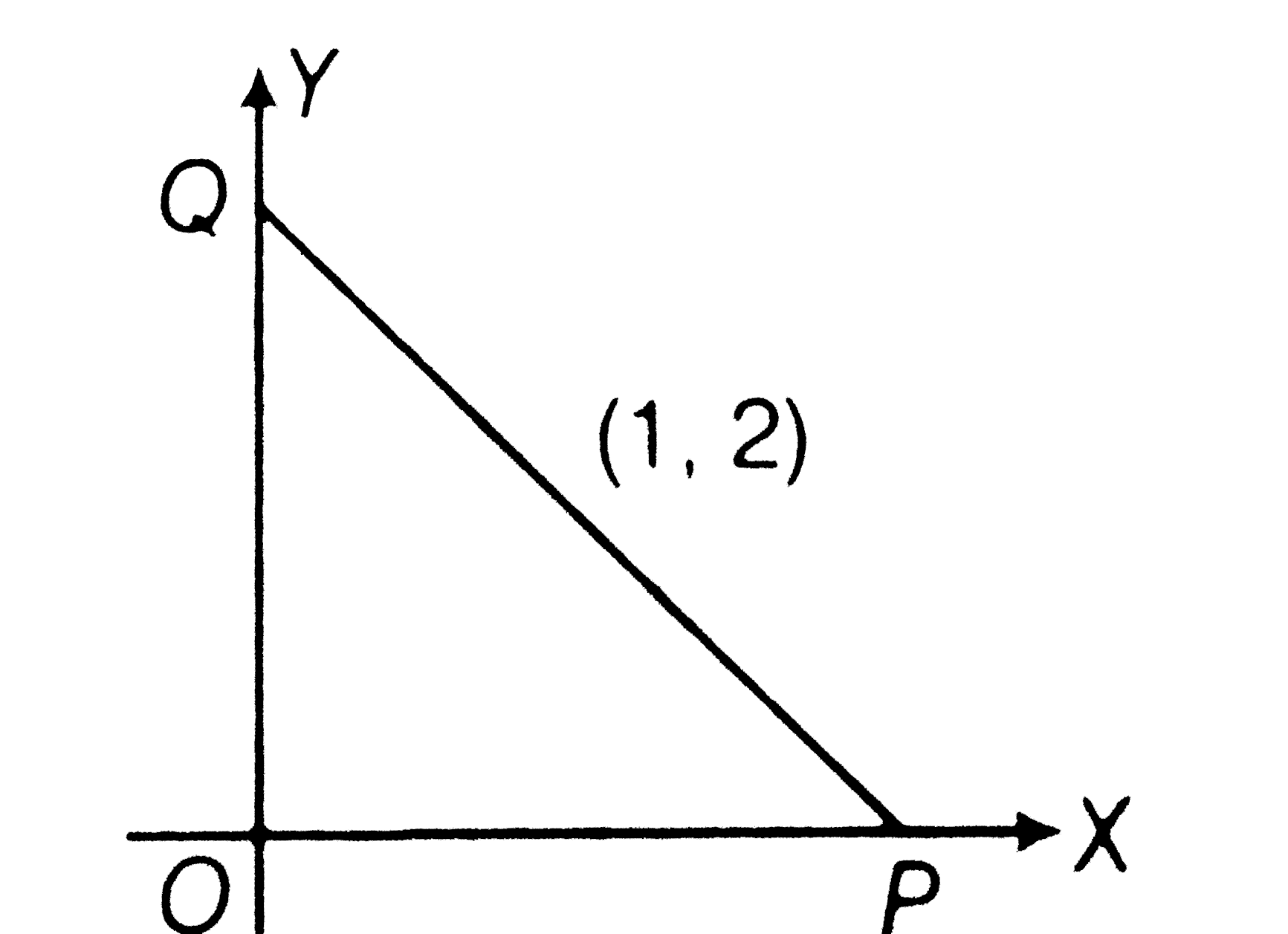
- A line is drawn through the point (1, 2) to meet the coordinate axes ...
Text Solution
|
- Rolle's theorem is not applicable for the function f(x)=|x| in the int...
Text Solution
|
- Find the slope of the normal to the curve y=x^2-1/(x^2) at (-1, 0)
Text Solution
|
- Suppose the cubic x^(3)-px+q has three distinct real roots, where pgt0...
Text Solution
|
- log(10) (4.04), it being given that log(10) 4 = 0.6021 and log(10) e =...
Text Solution
|
- The radius of a cylinder is increasing at the rate of 3ms^(-1) and its...
Text Solution
|
- A missile is fired from the ground level rises x metres vertically upw...
Text Solution
|
- If the radius of a circle be increasing at a uniform rate of 2cms^(-1)...
Text Solution
|
- The normal to the curve x=a ( cos theta-thetasintheta), y = a( sinthet...
Text Solution
|
- If ST and SN are the lengths of the subtangent and the subnormal at th...
Text Solution
|
- If a and b are positive quantities, (a gt b) find minimum positive val...
Text Solution
|
- The real number x when added to its inverse given the minimum value of...
Text Solution
|
- For which interval, the function (x^2-3x)/(x-1) satisfies all the cond...
Text Solution
|
- The value of c in (0,2) satisfying the Mean Value theorem for the func...
Text Solution
|
- For what values of x the function f(x)=x^(4)-4x^(3)+4x^(2)+40 is monot...
Text Solution
|
- If x in (0,pi//2), then the function f(x)= x sin x +cosx +cos^(2)x is
Text Solution
|
- Let k and K be the minimum and the maximum values of the function f(x)...
Text Solution
|
- If for a function f(x),f'(a)=0,f' ' (a)=0,f'''(a)gt0, then at x=a,f(x)...
Text Solution
|