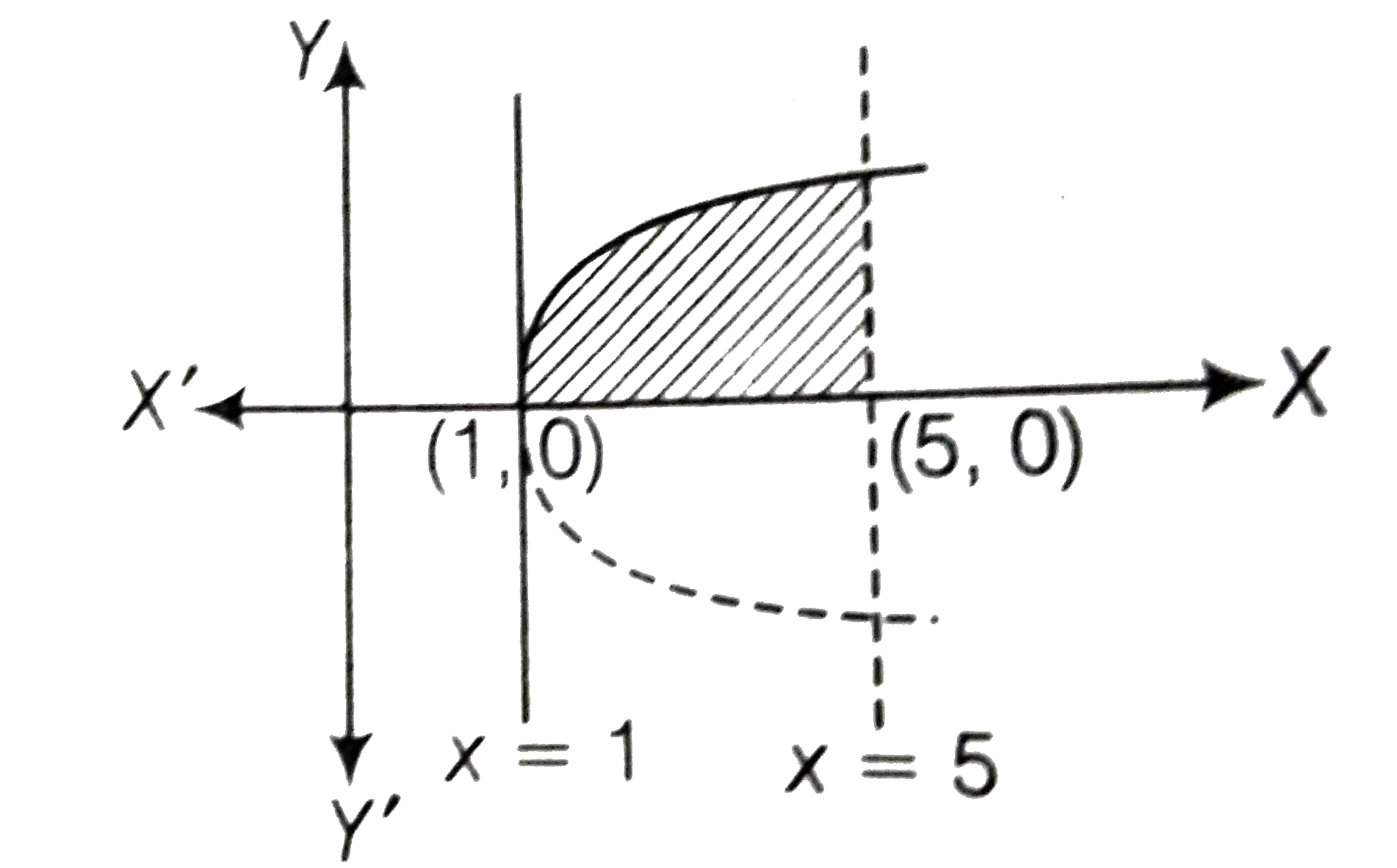A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATIONS OF DEFINITE INTEGRALS
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 VideosAPPLICATIONS OF DEFINITE INTEGRALS
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 VideosAPPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -Exercise 2
- Find the area under the curve y = sqrt(x-1) in the interval [1, 5] bet...
Text Solution
|
- If a curve y = asqrt(x)+bx passes through the point (1,2) and the area...
Text Solution
|
- What is the area bounded by the curves y=e^x ,y =e ^-x and the straig...
Text Solution
|
- The area between the curve y=2x^(4)-x^(2), the x-axis, and the ordinat...
Text Solution
|
- The area bounded by the curve y =ln(x) and the lines y = 0, y =ln(3) a...
Text Solution
|
- The area bounded between the parabolas x^2=y/4"and"x^2=9y and the s...
Text Solution
|
- The area of the figure bounded by the curves y^(2)=2x+1 and x-y-1=0 , ...
Text Solution
|
- The area of the plane region bounded by the curves x + 2y^(2)=0 and x+...
Text Solution
|
- The area enclosed between the curves y = x^(3) and y = sqrt(x) is
Text Solution
|
- The area enclosed between the parabola y = x^(2)-x+2 and the line y = ...
Text Solution
|
- The area bounded by the curves y^(2)=4a^(2)(x-1) and lines x = 1 and y...
Text Solution
|
- The area bounded by the curves y = cos x and y = sin x between the ord...
Text Solution
|
- The area of the plane region bounded by the curve x = y^(2)-2 and the ...
Text Solution
|
- The area bounded by the curve y = 2x - x^(2) and the line y = - x is
Text Solution
|
- For 0 lt= x lt= pi, the area bounded by y = x and y = x + sin x, is
Text Solution
|
- If the area above the x-axis, bounded by the curves y = 2^(kx) and x =...
Text Solution
|
- The area of the region described by A = {(x,y) : x^2 + y^2 lt= 1and y^...
Text Solution
|
- The area in the first quadrant between x^2+y^2=pi^2 and y=sinx is
Text Solution
|
- The area bounded by the curves y=sqrtx, 2y-x+3=0, X-axis and lying in ...
Text Solution
|
- The area bounded by y = |sin x|, X-axis and the line |x|=pi is
Text Solution
|