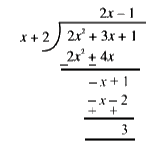Text Solution
Verified by Experts
Topper's Solved these Questions
MATHEMATICAL LOGIC
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE 2 OR 3 MARKS EACH|24 VideosMATHEMATICAL LOGIC
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE 3 MARKS EACH|4 VideosLINEAR PROGRAMMING
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE|8 VideosMATRICES
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise MULTIPLE CHOICE QUESTIONS|12 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-MATHEMATICAL LOGIC-MULTIPLE CHOICE QUESTIONS 2 MARKS EACH
- Determine whether each of the following statement patterns is a tautol...
Text Solution
|
- The converse of the contrapriate of ptoq is.
Text Solution
|
- The negation of the statement : ''If a person is social, then he is ha...
Text Solution
|
- The negation of ~p^^(qtor) is
Text Solution
|
- The negation of ~pto(qvvr) is
Text Solution
|
- If p^^q=F,ptoq=F then the truth values of p and q are
Text Solution
|
- Negation of ''AuuB=B is the sufficient condition for AsubeB'' is
Text Solution
|
- If A={2,3,4,5,6}, Then which of the following is not true ?
Text Solution
|
- The negation of inverse of ~ptoq is
Text Solution
|
- Inverse of statement pattern (pvvq)to(p^^q) is
Text Solution
|
- pto(qtor) is logically equivalent to
Text Solution
|