Consider a rigid body rotating with a constant angular velocity `vecomega` about an axis through the point O and perpendicular to the plane of the figure. Suppose that the body consists of N particles of masses `m_(1), m_(2), …, m_(N)` situated at distances `r_(1), r_(2), ..., r_(N)` respectively from tha axis of rotation as shown in the figure.
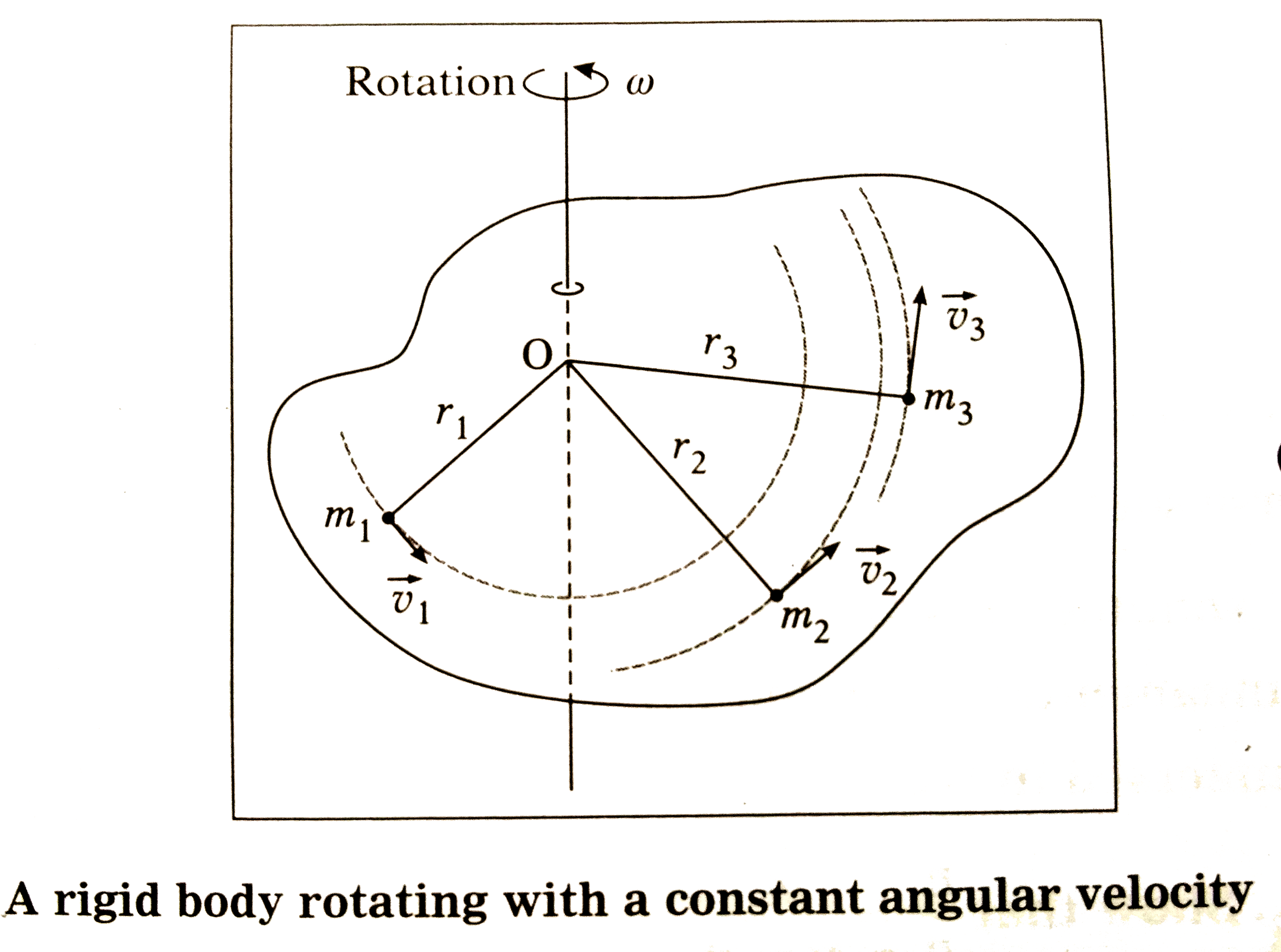
A rigid body rotating with a constant angular velocity
As the body rotates , all the particles perform uniform circular motion with the same angular velocity `vecomega` . However , various particles of the body have different linear speeds depending upon their distances from the axis of rotation .
The linear speed of the particle with mass ` m_(1) " is " v_(1) = r_(1) omega`. Therefore, its kinetic energy is
`E_(1) = 1/2 m_(1)v_(1)^(2) = 1/2 m_(1) r_(1)^(2) omega^(2)` ...(1)
Similarly , the kinetic energy of the particle with mass `m_(2) ` is
`E_(2) = 1/2 m_(2) v_(2)^(2) = 1/2 m_(2) r_(2)^(2) omega^(2)`,and so on .
The rotational kinetic energy (E) of the body is
` E = E_(1) + E_(2) + ... + E_(N)`
` = 1/2 m_(1) r_(1)^(2) omega^(2) + 1/2 m_(2) r_(2)^(2) omega^(2) + ... + 1/2 m_(N) r_(N)^(2) omega^(2) `
` = 1/2 [m_(1) r_(1)^(2) + m_(2) r_(2)^(2) + ... + m_(N) r_(N)^(2) ] omega^(2) = 1/2 (underset(i=1)overset(N) sum m_(i) r_(i)^(2)) omega^(2)`
` :. E = 1/2 Iomega^(2) ` ....(2)
where ` I = underset(i=1)overset(N) sum m_(i)r_(i)^(2)` is the moment of inertia of the body about the axis of rotation.
If f is the frequency of rotation of the body and T the period of rotation, then ` omega = 2 pi f = (2 pi)/T`
` :. E = 1/2 I (2 pi f)^(2) = 2 pi^(2) I f^(2) = 2 pi^(2) I/T^(2) ` ....(3)
Thus, from Eqs. (2) and (3) , the rotational kinetic energy of a body is proportional to (1) its moment of inertia about the given rotation axis (2) the square of its angular speed ( or frequency of rotation ) or inverse square of its rotational period .
