Similar Questions
Explore conceptually related problems
Recommended Questions
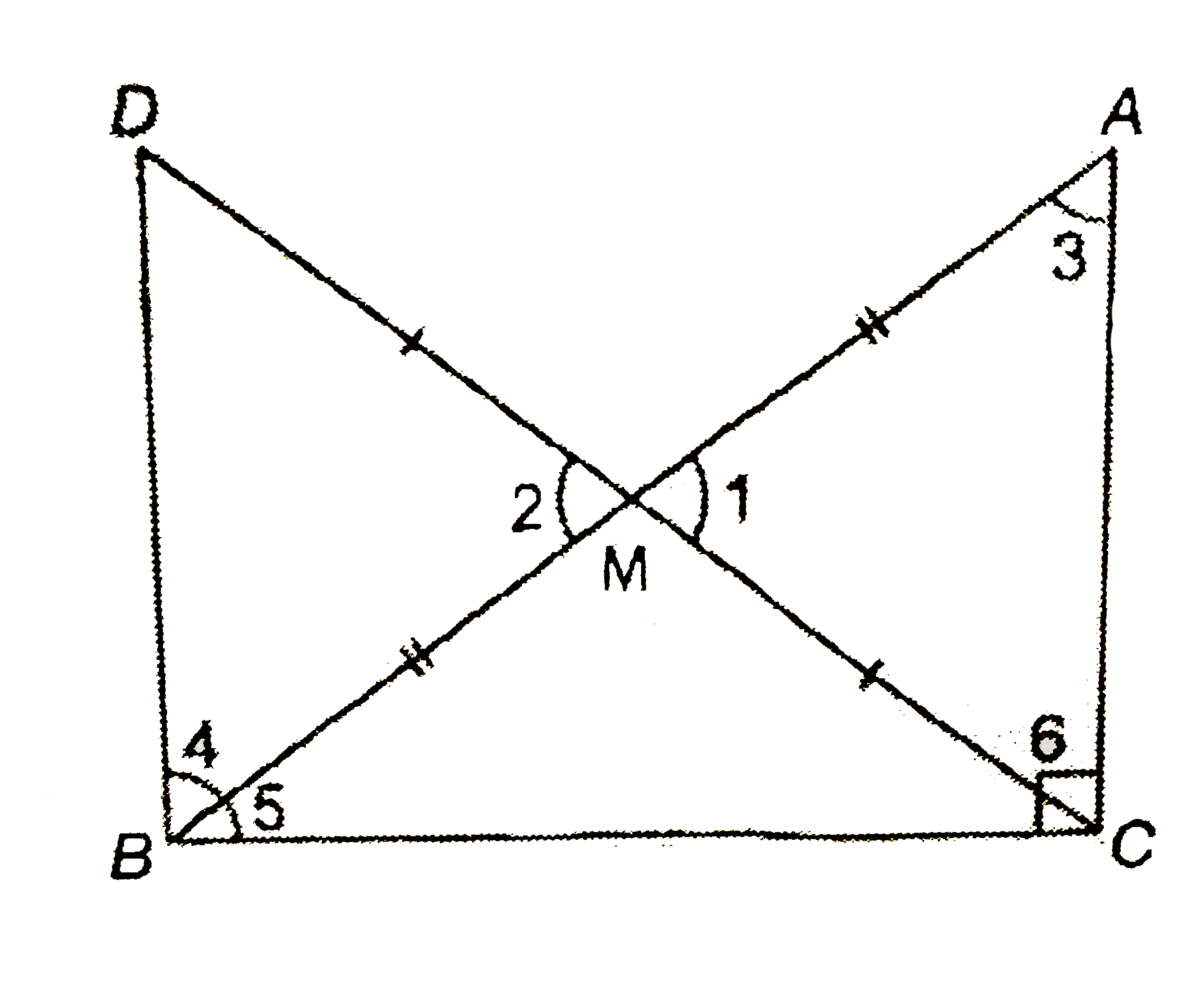
- In right triangle ABC, right angle at C, M is the mid-point of the hyd...
Text Solution
|
- In right triangle ABC, right angle at C, M is the mid-point of the hyd...
Text Solution
|
- एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बि...
Text Solution
|
- एक समकोण त्रिभुज ABC में, C समकोण है, कर्ण AB का मध्य बिन्दु M है | C ...
Text Solution
|
- In right triangle ABC, right angled at C, M is the mid-point of hypote...
Text Solution
|
- In right triangle ABC, right angle is at C, M is the mid-point of hypo...
Text Solution
|
- In right triangle ABC, right angle is at C, M is the mid-point of hypo...
Text Solution
|
- In right triangle ABC, right angle is at C, M is the mid-point of hypo...
Text Solution
|
- एक समकोण त्रिभुज ABC में, जिसमे कोण C समकोण है, M कोण AB का मध्य बिन्द...
Text Solution
|