Home
Class 9
MATHS
Theorem 7.6 : If two sides of a triangle...

Theorem 7.6 : If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater)

Text Solution

Verified by Experts


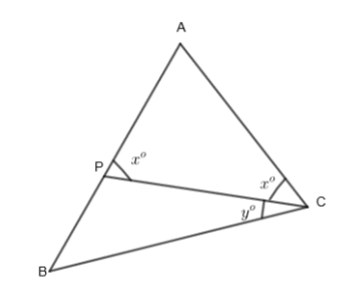
Let us assume a triangle `ABC` such that the sides are as `AB > AC`.
Now, take a point `P` on line `AB` such that `AP = AC`. Join the two points `C` and `P` to set `CP`. Let us assume angle `APC` is `x` and angle `BCP` is `y`.
. We know that `AP = AC`.
If two sides are equal in a triangle, then the angles opposite to the sides are equal. Applying this condition to the triangle `APC`, we get the angle `APC` and angle `ACP`, all equal. As angle `APC` is `x`,
we get the angle `ACP` also `x`.
Mathematically, we write these steps as follows:
`/_ACP=/_APC`
...
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

If two angles of a triangle are equal;then sides opposite to them are also equal.

If two sides of a triangle are unequal; the longer side has greater angle opposite to it.

In a triangle the angle opposite the largest side is the largest.

In a triangle the greater angle has the longer side opposite to it.

Fill in the blanks to make the following statements true: In a right triangle the hypotenuse is the ...... side. The sum of three altitudes of a triangle is ......... than its perimeter. The sum of any two sides of a triangle is ......... than the third side. If two angles of a triangle are unequal, then the smaller angle has the ........... side opposite to it. Difference of any two sides of a triangle is ......... than the third side. If two sides of a triangle are unequal, then the larger side has ..... angle opposite to it.

Which of the following statements are true (T) and which are false (F)? Sum of the three sides of a triangle is less than the sum of its three altitudes. Sum of any two sides of a triangle is greater than twice the median drawn to the third side. Sum of any two sides of a triangle is greater than the third side. Difference of any two sides of a triangle is equal to the third side. If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it. Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.

If two angles of a triangle are unequal , then the smaller angle has the ________ side opposite to it .

Theorem 7.8 : The sum of any two sides of a triangle is greater than the third side.