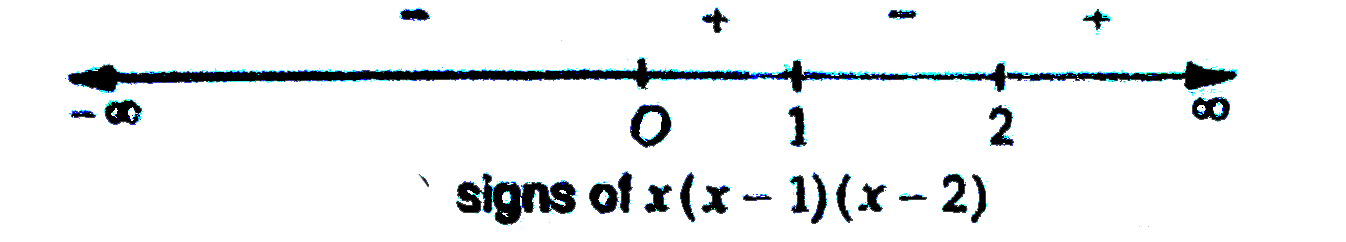A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DEFINITE INTEGRALS
OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|12 VideosDEFINITE INTEGRALS
OBJECTIVE RD SHARMA|Exercise Exercise|147 VideosDEFINITE INTEGRALS
OBJECTIVE RD SHARMA|Exercise Chapter Test 2|60 VideosCONTINUITY AND DIFFERENTIABILITY
OBJECTIVE RD SHARMA|Exercise Exercise|86 VideosDERIVATIVE AS A RATE MEASURER
OBJECTIVE RD SHARMA|Exercise Exercise|26 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA-DEFINITE INTEGRALS-Section I - Solved Mcqs
- int(0)^(10)|x(x-1)(x-2)|dx is equal to
Text Solution
|
- If int(0) ^(x) f (t) dt = x + int (x ) ^(1) t f (t) dt, then the v...
Text Solution
|
- Let f be a positive function. Let I1 = int(1-k)^(k) xf{x(1-x}dx, I(2...
Text Solution
|
- If g(x)=int(0)^(x)cos^(4) dt, then g(x+pi) equals
Text Solution
|
- If l(n)=int(0)^(pi//4) tan^(n)x dx, n in N "then" I(n+2)+I(n) equals
Text Solution
|
- If rArr I(n)=int(0)^(pi//4) tan ^(n)x dx, then for any positive integ...
Text Solution
|
- The value of int(-1)^(1) (d)/(dx) ("tan"^(1)(1)/(x))dx is
Text Solution
|
- The vlaue of the integral int(-1)^(3) ("tan"^(1)(x)/(x^(2)+1)+"tan"^...
Text Solution
|
- If =int(1)^(e) (logx)^(n) dx, "then"I(n)+nI(n-1) is equal to
Text Solution
|
- If =int(0)^(1) x^(n)e^(-x)dx "for" n in N "then" I(n)-nI(n-1)=
Text Solution
|
- The value of int(1//n)^((an-1)//n) (sqrt(x))/(sqrt(a-x+sqrtx))dx, is
Text Solution
|
- The value of the integral int(0)^(pi//2)log |tan x cot x |dx is
Text Solution
|
- If I(1)=int(x)^(1)(1)/(1+t^(2)) dt and I(2)=int(1)^(1//x) dt "for" x g...
Text Solution
|
- For all values of , int(1//e)^(tanx) (t)/(1+t^(2))dt+int(1//e)^(tanx) ...
Text Solution
|
- The absolute value of int(10)^(19) (cosx)/(1+x^(8))dx, is
Text Solution
|
- If f(x) is an odd pefiodc function defined on the interval [T/2,T/2], ...
Text Solution
|
- If int(pi//2)^(theta) sin x dx=sin 2 theta then the of theta satisfyin...
Text Solution
|
- If f(x) is periodic function with period, T, then
Text Solution
|
- If f(n)=(1)/(n){(n+1)(n+2)(n+3)...(n+n)}^(1//n) then lim(n to oo)f(n)...
Text Solution
|
- The poins of extremum of phi(x)=int(1)^(x) e^(-t^(2)//2) (1-t^(2))dt a...
Text Solution
|