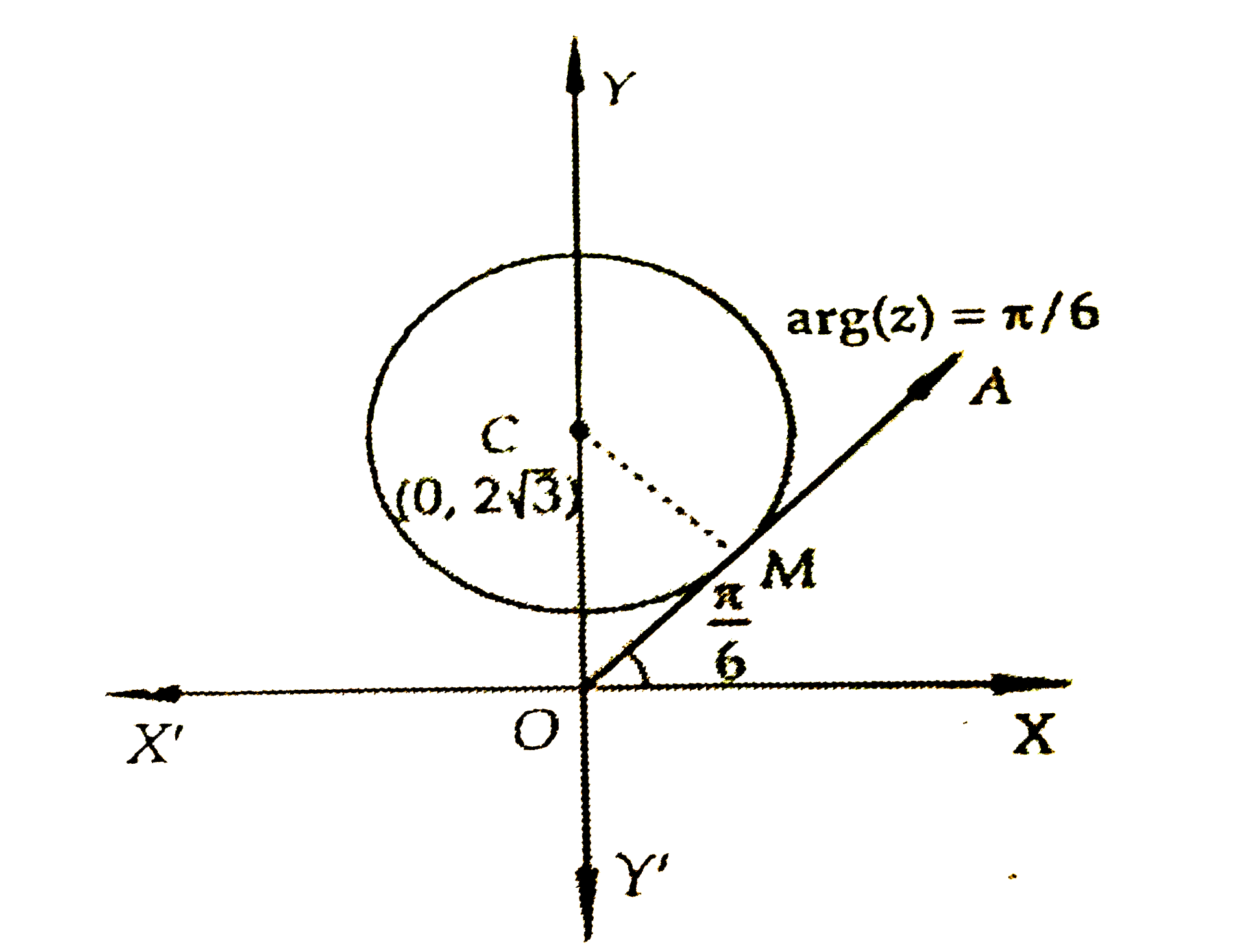The least value of p for which the two c...

The least value of p for which the two curves `arg z=pi/6` and `|z-2sqrt(3)i|=p` intersect is

`sqrt(3)`

`1//sqrt(3)`

`1//3`

Text Solution

Verified by Experts

The correct Answer is:

The equation `|z-2sqrt(3)i|=p` represents a circle of radius p having center at C`(0,2sqrt(3))` and arg(z) `=pi//6` is a line making an angle of `30^(@)` with OX and lying in first quadrant

Let CM be perpendicular from C on OA. Then,
CM=OC`sinpi/3=2sqrt(3) xx sqrt(3)/2=3`
Clearly, the two curves will intersect, if
`CM le p rArr 3 le p rArr p ge 3`.
Hence, the least value of p is 3.

Topper's Solved these Questions

COMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Section I - Solved Mcqs|141 Videos
COMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|15 Videos
CIRCLES
OBJECTIVE RD SHARMA|Exercise Chapter Test|55 Videos
CONTINUITY AND DIFFERENTIABILITY
OBJECTIVE RD SHARMA|Exercise Exercise|86 Videos

Similar Questions

Explore conceptually related problems

The least value of p for which the two curves argz=(pi)/(6) and |z-2sqrt(3)i|=p intersect is

Given that the two curves a r g(z)=pi/6a n d|z-2sqrt(3)i|=r intersect in two distinct points, then [r]!=2 b. 0

The mirror image of the curve arg((z-3)/(z-i))=(pi)/(6),i=sqrt(-1) in the real axis

Find the value of z, if |z |= 4 and arg (z) = (5pi)/(6) .

if arg(z+a)=(pi)/(6) and arg(z-a)=(2 pi)/(3) then

Find the point of intersection of the curves arg(z-3i)=(3 pi)/(4) and arg (2z+1-2i)=pi/4

Number of z, which satisfy Arg(z-3-2i)=(pi)/(6) and Arg(z-3-4i)=(2 pi)/(3) is/are :

Let A(z_(1)) be the point of intersection of curves arg(z-2+i)=(3 pi)/(4)) and arg(z+i sqrt(3))=(pi)/(3),B(z_(2)) be the point on the curve ar g(z+i sqrt(3))=(pi)/(3) such that |z_(2)-5|=3 is minimum and C(z_(2)) be the centre of circle |z-5|=3. The area of triangle ABC is equal to

OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Chapter Test

The least value of p for which the two curves arg z=pi/6 and |z-2sqrt...
Text Solution
|
The locus of the center of a circle which touches the circles |z-z1|=a...
Text Solution
|
If n1, n2 are positive integers, then (1 + i)^(n1) + ( 1 + i^3)^(n1) +...
Text Solution
|
The modulus of sqrt(2i)-sqrt(-2i) is
Text Solution
|
Prove that the triangle formed by the points 1,(1+i)/(sqrt(2)),a n di ...
Text Solution
|
The value of (1+isqrt(3))/(1-isqrt(3))^(6)+(1-isqrt(3))/(1+isqrt(3))^(...
Text Solution
|
If alpha+ibeta=tan^(-1) (z), z=x+iy and alpha is constant, the locus o...
Text Solution
|
If cosA+cosB+cosC=0,sinA + sinB + sinC=0and A+B+C=180^0, then the valu...
Text Solution
|
The value of the expression 1.(2-omega).(2-omega^2)+2.(3-omega)(3-omeg...
Text Solution
|
The value of the expression (1+1/omega)(1+1/omega^(2))+(2+1/omega)(2+...
Text Solution
|
The condition that x^(n+1)-x^(n)+1 shall be divisible by x^(2)-x+1 is ...
Text Solution
|
The expression (1+i)^(n1)+(1+i^(3))^(n(2)) is real iff
Text Solution
|
|{:("6i " "-3i " "1" ),("4 " " 3i" " -1"),("20 " "3 " " i"):}|=x+iy th...
Text Solution
|
The centre of a square ABCD is at z0dot If A is z1 , then the centroid...
Text Solution
|
If cosalpha+2cosbeta+3cosgamma=sinalpha+2sinbeta+3singamma=0 and alpha...
Text Solution
|
If cosalpha+2cosbeta+3cosgamma=sinalpha+2sinbeta+3singamma=0 and alpha...
Text Solution
|
Sum of the series sum(r=0)^n (-1)^r ^nCr[i^(5r)+i^(6r)+i^(7r)+i^(8r)] ...
Text Solution
|
If az(1)+bz(2)+cz(3)=0 for complex numbers z(1),z(2),z(3) and real num...
Text Solution
|
If 2z1-3z2 + z3=0, then z1, z2 and z3 are represented by
Text Solution
|
Re((z+4)/(2z-1)) = 1/2, then z is represented by a point lying on
Text Solution
|
The vertices of a square are z1,z2,z3 and z4 taken in the anticlockwis...
Text Solution
|