Home
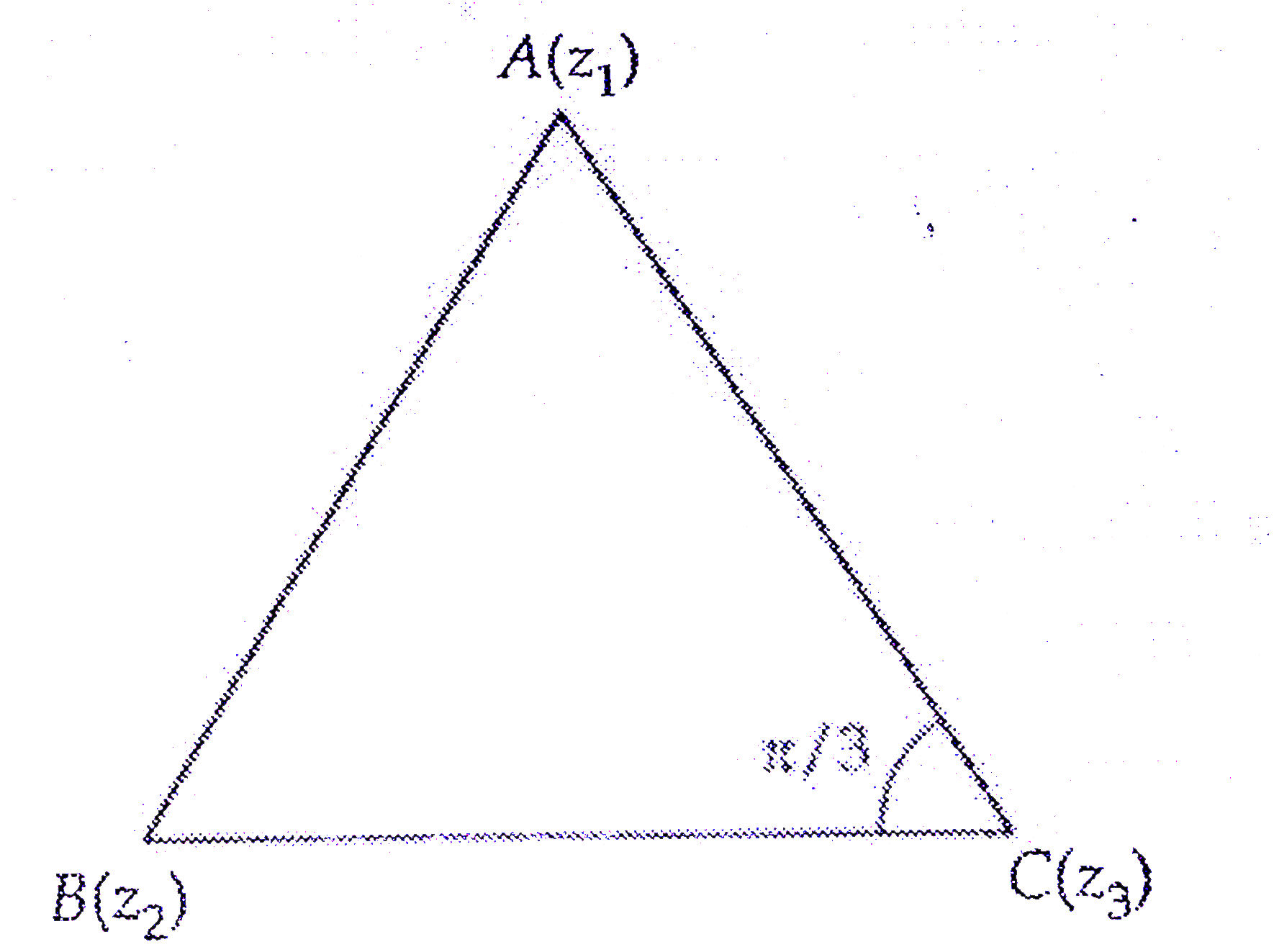
Class 12
MATHS
The complex number z1,z2 and z3 satisfyi...

The complex number `z_1,z_2 and z_3` satisfying `(z_1 - z_3)/(z_2 - z_3) = ( 1 - i sqrt3)/2` are the vertices of a triangle which is :

A

of area zero

B

right-angled isosceles

C

equilateral

D

obtuse-angled isosceles

Text Solution

Verified by Experts

The correct Answer is:
C
We have,
`(z_(1)-z_(3))/(z_(2)-z_(3))=(1-isqrt(3))/(2)`

`rArr (z_(1)-z_(3))=e^(-pi//3)(z_(2)-z_(3))`.
`rArr bar(CA)` is obtained by rotating `bar(CB)` through `pi//3` in clockwise sense.
`rArr` CA=CB and `angleAOB=pi/3`
`rArr triangleABC` is an equilateral triangle.
Promotional Banner

Topper's Solved these Questions

  • COMPLEX NUMBERS

    OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|15 Videos

  • COMPLEX NUMBERS

    OBJECTIVE RD SHARMA|Exercise Exercise|131 Videos

  • COMPLEX NUMBERS

    OBJECTIVE RD SHARMA|Exercise Chapter Test|59 Videos

  • CIRCLES

    OBJECTIVE RD SHARMA|Exercise Chapter Test|55 Videos

  • CONTINUITY AND DIFFERENTIABILITY

    OBJECTIVE RD SHARMA|Exercise Exercise|86 Videos

Similar Questions

Explore conceptually related problems

The complex numbers z_1 z_2 and z3 satisfying (z_1-z_3)/(z_2-z_3) =(1- i sqrt(3))/2 are the vertices of triangle which is (1) of area zero (2) right angled isosceles(3) equilateral (4) obtuse angled isosceles

The complex number z_(1),z_(2) and z_(3) satisfying (z_(1)-z_(3))/(z_(2)-z_(3))=(1-i sqrt(3))/(2) are the vertices of a triangle which is :

Complex number z_1, z_2 and z_3 in AP

The complex numbers z_(1),z_(2),z_(3) stisfying (z_(2)=z_(3))=(1+i)(z_(1)-z_(3)).where i=sqrt(-1), are vertices of a triangle which is

For complex numbers z_1 = 6+3i, z_2=3-I find (z_1)/(z_2)

Let z_1 , z _2 and z_3 be three complex numbers such that z_1 + z_2+ z_3 = z_1z_2 + z_2z_3 + z_1 z_3 = z_1 z_2z_3 = 1 . Then the area of triangle formed by points A(z_1 ), B(z_2) and C(z_3) in complex plane is _______.

OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Section I - Solved Mcqs
  1. If z(1),z(2),……………,z(n) lie on the circle |z|=R, then |z(1)+z(2)+………...

    Text Solution

    |

  2. Q. Let z1 and z2 be nth roots of unity which subtend a right angle at...

    Text Solution

    |

  3. The complex number z1,z2 and z3 satisfying (z1 - z3)/(z2 - z3) = ( 1 -...

    Text Solution

    |

  4. Let omega = - (1)/(2) + i (sqrt3)/(2), then the value of the determina...

    Text Solution

    |

  5. For all complex numbers z1,z2 satisfying |z1|=12 and |z2-3-4i|=5, fin...

    Text Solution

    |

  6. Let z1, z2 be two complex numbers represented by points on the circle ...

    Text Solution

    |

  7. If z lies on unit circle with center at the origin, then (1+z)/(1+barz...

    Text Solution

    |

  8. If |z1-1|<1, |z2-2|<2,|z3-3|<3 then |z1+z2+z3|

    Text Solution

    |

  9. Complex numbers z(1) and z(2) lie on the rays arg(z1)=theta and arg(z1...

    Text Solution

    |

  10. If z is a complex number satisfying |z|^(2)-|z|-2 lt 0, then the value...

    Text Solution

    |

  11. |z - i | <= 2 and z0 = 5 + 3i then max. value of |iz+z0| is :

    Text Solution

    |

  12. If |z|= "max"{|z-2|,|z+2|}, then

    Text Solution

    |

  13. if |(z-6)/(z+8)|=1, then the value of x in R, where z=x+i|{:(-3,2i,2+i...

    Text Solution

    |

  14. If |z-1|+|z+3|<=8, then the range of values of |z-4| is

    Text Solution

    |

  15. The equation |z-i|+|z+i|=k, k gt 0 can represent an ellipse, if k=

    Text Solution

    |

  16. Find the range of K for which the equation |z+i| - |z-i | = K represen...

    Text Solution

    |

  17. If |z+3i|+|z-i|=8, then the locus of z, in the Argand plane, is

    Text Solution

    |

  18. In Fig. 42, a point 'z' is equidistant from three distinct points z(1)...

    Text Solution

    |

  19. Let P(e^(itheta1)), Q(e^(itheta2)) and R(e^(itheta3)) be the vertices...

    Text Solution

    |

  20. If A(z(1)),B(z(2)), C(z(3)) are the vertices of an equilateral triangl...

    Text Solution

    |