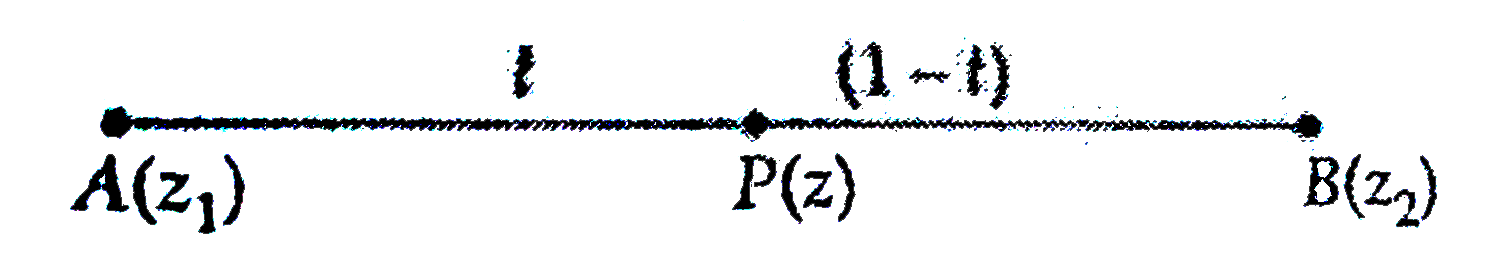A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|15 VideosCOMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Exercise|131 VideosCOMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Chapter Test|59 VideosCIRCLES
OBJECTIVE RD SHARMA|Exercise Chapter Test|55 VideosCONTINUITY AND DIFFERENTIABILITY
OBJECTIVE RD SHARMA|Exercise Exercise|86 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Section I - Solved Mcqs
- If 0 le "arg"(z) le pi/4, then the least value of |z-i|, is
Text Solution
|
- If |z1|+|z2|=1 and z1+z2+z3=0 then the area of the triangle whose vert...
Text Solution
|
- Let Z1 and Z2, be two distinct complex numbers and let w = (1 - t) z1 ...
Text Solution
|
- Let omega be the complex number cos((2pi)/3)+isin((2pi)/3). Then the...
Text Solution
|
- The set of points z in the complex plane satisfying |z-i|z||=|z+i|z|| ...
Text Solution
|
- The set of points z satisfying |z+4|+|z-4|=10 is contained or equal to
Text Solution
|
- If |omega|=2, then the set of points z=omega-1/omega is contained in o...
Text Solution
|
- If |omega|=1, then the set of points z=omega+1/omega is contained in o...
Text Solution
|
- The number of complex numbers z such that |z-1|=|z+1|=|z-i| is
Text Solution
|
- Let alpha and beta be real numbers and z be a complex number. If z^(2...
Text Solution
|
- If omega !=1 is the complex cube root of unity and matrix H=[(omega,...
Text Solution
|
- The maximum value of |a r g(1/(1-z))|for|z|=1,z!=1 is given by.
Text Solution
|
- If z is any complex number satisfying |z-3-2i|lt=2 then the maximum va...
Text Solution
|
- Let omega be the solution of x^(3)-1=0 with "Im"(omega) gt 0. If a=2 w...
Text Solution
|
- The set {R e((2i z)/(1-z^2)): zi sacom p l e xnu m b e r ,|z|=1,z=+-1}...
Text Solution
|
- Let omega= e^((ipi)/3) and a, b, c, x, y, z be non-zero complex numb...
Text Solution
|
- The minimum value of |z(1)-z(2)| as z(1) and z(2) vary over the curves...
Text Solution
|
- Let complex numbers alpha and 1/alpha lies on circle (x-x0)^2(y-y0)^2=...
Text Solution
|
- Let w = (sqrt 3 + iota/2) and P = { w^n : n = 1,2,3, ..... }, Further ...
Text Solution
|
- Let S=S1 nn S2 nn S3, where s1={z in C :|z|<4}, S2={z in C :ln[(z-...
Text Solution
|