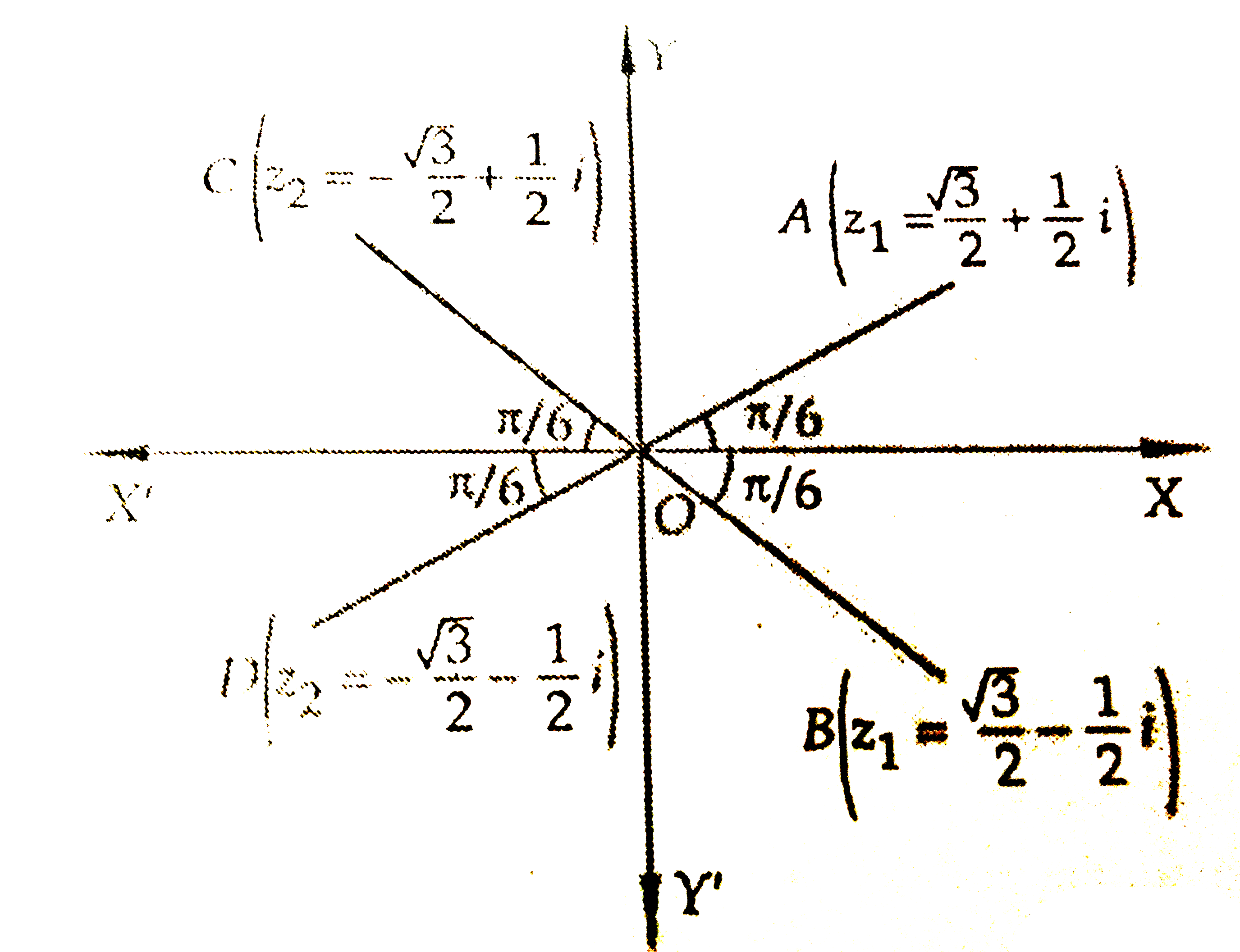
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|15 VideosCOMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Exercise|131 VideosCOMPLEX NUMBERS
OBJECTIVE RD SHARMA|Exercise Chapter Test|59 VideosCIRCLES
OBJECTIVE RD SHARMA|Exercise Chapter Test|55 VideosCONTINUITY AND DIFFERENTIABILITY
OBJECTIVE RD SHARMA|Exercise Exercise|86 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Section I - Solved Mcqs
- The minimum value of |z(1)-z(2)| as z(1) and z(2) vary over the curves...
Text Solution
|
- Let complex numbers alpha and 1/alpha lies on circle (x-x0)^2(y-y0)^2=...
Text Solution
|
- Let w = (sqrt 3 + iota/2) and P = { w^n : n = 1,2,3, ..... }, Further ...
Text Solution
|
- Let S=S1 nn S2 nn S3, where s1={z in C :|z|<4}, S2={z in C :ln[(z-...
Text Solution
|
- Let S=S1 nn S2 nn S3, where s1={z in C :|z|<4}, S2={z in C :ln[(z-...
Text Solution
|
- Let z(k)=cos(2kpi)/10+isin(2kpi)/10,k=1,2,………..,9. Then, 1/10{|1-z(1)|...
Text Solution
|
- In Q. No. 121, 1-sum(k=1)^(9)cos(2kpi)/10 equals
Text Solution
|
- If z is a complex number such that |z|>=2 then the minimum value of |z...
Text Solution
|
- A complex number z is said to be uni-modular if |z|=1. Suppose z(1) a...
Text Solution
|
- If |z-2-i|=|z|sin(pi/4-a r g z)| , where i=sqrt(-1) ,then locus of z,...
Text Solution
|
- f(n) = cot^2 (pi/n) + cot^2\ (2 pi)/n +...............+ cot^2\ ((n-1) ...
Text Solution
|
- If z(1) and z(2) are lying on |z-3| le 4 and |z-1|=|z+1|=3 respecivel...
Text Solution
|
- If |z-1| =1 and arg(z)=theta, where z ne 0 and theta is acute, then (1...
Text Solution
|
- If z is a complex number lying in the first quadrant such that "Re"(z)...
Text Solution
|
- The maximum area of the triangle formed by the complex coordinates z,...
Text Solution
|
- If z is a complex number satisfying |z|^(2)+2(z+2)+3i(z-barz)+4 =0, th...
Text Solution
|
- Locus of z if arg[z - (1 + i)] = {(3pi)/4 when |z|le|z-2| and (-pi)/4...
Text Solution
|
- Let z in C and if A={z:"arg"(z)=pi/4}and B={z:"arg"(z-3-3i)=(2pi)/3}. ...
Text Solution
|
- Let S={z in C:z(iz(1)+1,|z(1)| lt 1}. Then, for all z in S, which one ...
Text Solution
|
- Let z=1+ai be a complex number, a > 0,such that z^3 is a real number....
Text Solution
|