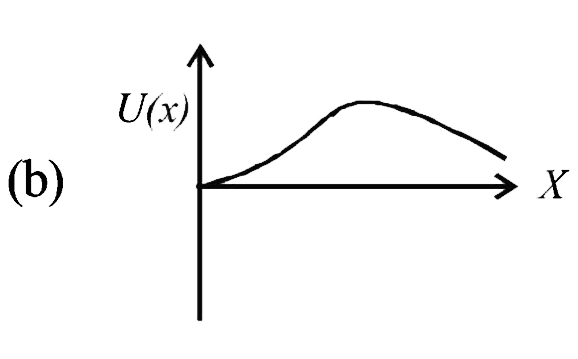
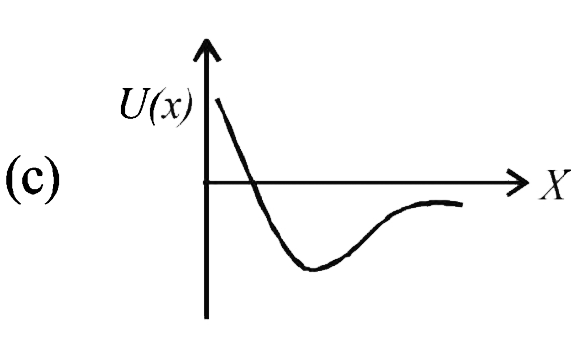
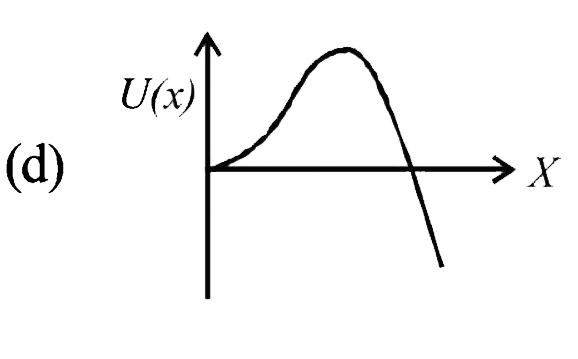
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNIL BATRA (41 YEARS IITJEE PHYSICS)-WORK, ENERGY & POWER-JEE Main And Advanced
- A spring of Force- constant K is cut into two pieces sach that one pie...
Text Solution
|
- A wind - powered generator convets and energy into electrical energy ...
Text Solution
|
- A particle which is constant to move along the x- axis , is subjected ...
Text Solution
|
- An ideal spring with spring - constant K is bung from the colling and...
Text Solution
|
- If W(1) W(2) and W(3) represent the work done in moving a particle fro...
Text Solution
|
- A particle is acted by x force F = Kx where K is a( + Ve) constant its...
Text Solution
|
- A block (B) is attached to two unstriched sprig S(1) and S(2) with spr...
Text Solution
|
- Two small particles of equal masses stant moving in opposite directio...
Text Solution
|
- A piece of wire is bent in the shape of a parabola y = Kx^(2) (y - axi...
Text Solution
|
- A block of mass2 kg is from to move along the x - axis it is at rest...
Text Solution
|
- The work done an a particle of mass m by a force K[(x)/((x^(2) + y^(...
Text Solution
|
- A tennis ball dropped on a barizoontal smooth surface , it because bac...
Text Solution
|
- A body is moved along a straight line by a machine delivering constant...
Text Solution
|
- A uniform chain of length L and mass M is tying on a smoth table and o...
Text Solution
|
- A particle is acted upen by the a force of constant magninude which is...
Text Solution
|
- A force F = -K(y hatI + x hatj)(where K is a posive constant ) acts on...
Text Solution
|
- A stone tied to a string of length L is whirled in a vertical circle w...
Text Solution
|
- A small bell starts moving from A over a fixed track as shown in the f...
Text Solution
|
- A bullet is fired from rifle . If the rifle recoils freely determine w...
Text Solution
|
- A spring of force constant k is cut into three equal parts what is for...
Text Solution
|