Home
Class 11
PHYSICS
A long horizontal rod has a bead which c...

A long horizontal rod has a bead which can slide along its length and initially placed at a
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration `alpha.` if the coefficient of friction between the rod and the bead is `mu`, and gravity is neglected, then the time after which the bead starts slipping is

A

`sqrt(mu//alpha)`

B

`mu//sqrtalpha`

C

`(1)/(sqrt(mu alpha)`

D

infinitesimal

Text Solution

Verified by Experts

The correct Answer is:
A
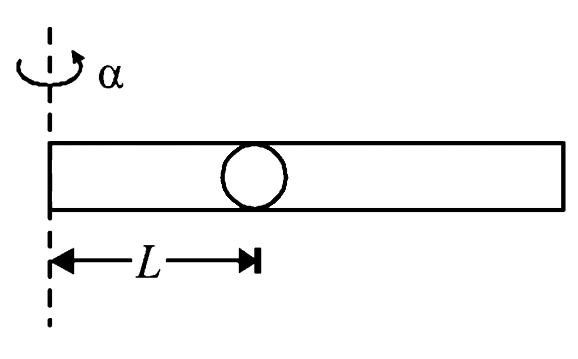
When we are giving an angular acceleration to
the rod, the bead is also having an instantanceous
acceleration `a = Lalpha.` This will happen when a force is
exerted on the bead by the rod. The bead has a tendency
to move away from the centre. But due to the friction
between the bead and the rod, this does not happen to
the extent to which frictional force is capable of holding
the bead.
The frictional force here provides the necessary
centripetal force. If instantaneous angular velocity is
`omega` then
`mLomega^2 = mu(ma) rArr mLomega^2 = mu mLalpha rArr omega^2 = mualpha`
By applying
`rArr omega = omega_0 + alphat,`
We get `omega =alphat`
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs with one correct answer|1 Videos

  • MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|63 Videos

  • SIMPLE HARMONIC MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|69 Videos

Similar Questions

Explore conceptually related problems

A rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is mu, find the value of I if the rod starts sliding.

A uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a//3 from the edge. The rod is released from rest. If the rod slips after it turned an angle theta , find the coefficient of friction between the rod and the table.

A bead is contrained to move on rod in granvity free space as shown in figure. The rod rotating with ,angular velocity and angulnr acceleration alpha about its end. If mu is coefficient of friction. Mark the correct option. ( Rod rotates in the plane of paper.)

L shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed omega .The sleeve has mass m and friction coefficient between rod and sleeve is mu .The minimum angular speed omega for which sleeve cannot slip on rod is?

In the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.

A rod is kept inclined at an angle theta with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is mu , for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?