A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -

Options

A. `4MR^2`
B. `(40)/(9) MR^2`
C. `10MR^2`
D. `(37)/(9)MR^2`

Answer

A

Explanation

(a) Let `sigma` be the mass per unit area.

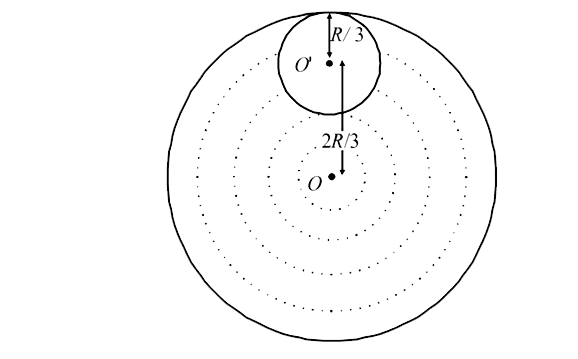
The total mass of the disc
`= sigmaxxpiR^2 = 9M`
The mass of the circular disc cut
`=alphaxxpi((R )/(3))^2 = alphaxx(piR)^2 /(9) = M`
Let us consider the above system as a complete disc of
mass 9M and a negative mass M super imposed on it.
Moment of inertia `(I_1)` of the complete disc =
`(1)/(2) 9 MR^2` about an axis passing through O and perpendicular to the plane of the disc.
M.I. of the cut out portion about an axis passing through
O and perpendicular to the plane of disc
`=(1)/(2)xxMxx((R )/(3))^2`
`:. M.I. (I_2)` of the cut portion about an axis passing
through O and perpendicular to the plane of disc
`=[(1)/(2)xxMxx((R )/(3))^2xxMxx((2R)/(3))^2]`
[Using perpendicular axis theorem]
`:.` The total M.I. of the system about an axis passing
through O and perpendicular to the plane of the disc is `I = I_1+I_2`
`=(1)/(2)9MR^2 - [(1)/(2)xxMxx((R )/(3))^2xMxx((2R)/(3))^2]`
`=(9MR^2)/(2)- (9MR^2)/(18) = (((9-1)) MR^2)/(2)` = 4MR^2`