(b) We know that `|vec tau| = |(dvecL)/(dt)| where L = I omega`
`:. tau = (d)/(dt)(Iomega) = omega(dl)/(dt) ….(i)`
From the situation it is clear that the moment of inerita
for (rod + insect) system is increasing.
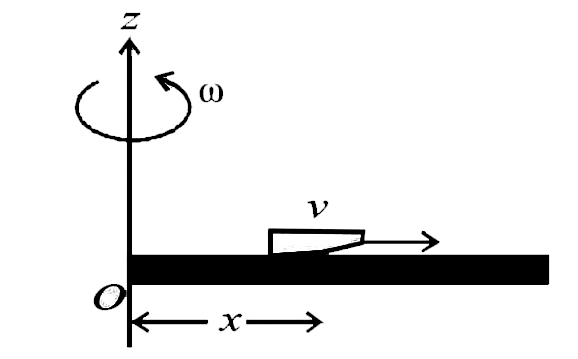
Let at any instant of time 't', the insect is at a distance x
from O. At this instant, the moment of inertia of the
system is
`I = (1)/(3) ML^2 + mx^2 ....(ii)` From (i)& (ii)
`tau = omega(d)/(dt) [(1)/(3) ML^2 + mx^2] = omegam (d)/(dt) (x^2)`
`=2 omega mx (dx)/(dt) = 2 omega mxu`
`=2omega mv^2 t`
`:. pi prop t`
When the inscet stops moving `vecL` does not change
and there fore `tau` becomes constant.