A solid cylinder is rolling down a rough inclined plane of inclination `theta`. Then

Options

A. The friction force is dissipative
B. The friction force is necessarily changing
C. The friction force will aid rotation but hinder translation
D. The friction force is reduced if `theta` is reduced

Answer

C, D

Explanation

(c,d) As showh in the figure, the compont of weight
mg `sin theta` tands to slide the point of contact (of the cylinder
with inclined plane) along its direction. The sliding friction
acts in the opposite direction to oppose this relative motion.
Because of frictional force the cylinder rolls.

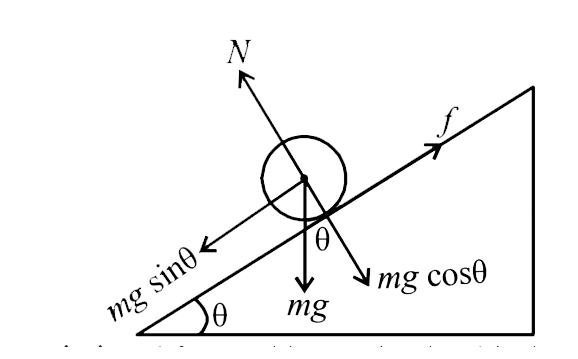
Thus frictional force adds rotation but hinders translational
motion.
Applying `F_(net) = ma` along the direction of the inclined plane,
we get `mg sin theta -f =o ma_(c,)`
Where `a_c`= acceleration of centre of mass of the cylinder
`:. f = mg sin theta - ma_c ....(i)`
But `a_c = (g sin theta)/( 1 + (I_c)/(mR^2) = (g sin theta )/(1+(mR^2//2)/(mR^2 ) = (2)/(3)g sin theta ....(ii)`
From (i) and (ii), f = (mg sin theta)/(3)`
if `theta` is reduced, frictional force is reduced.