Home
Class 11
PHYSICS
A ring of mass M and radius R is rotatin...

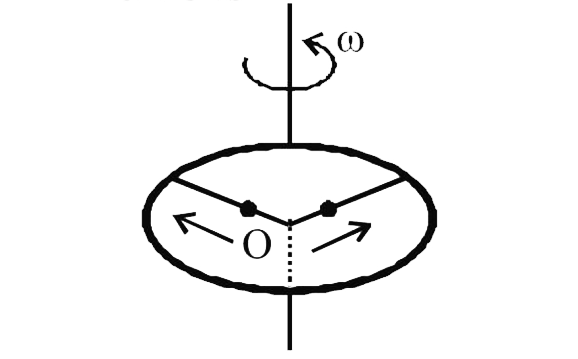
A ring of mass M and radius R is rotating with angular speed `omega` about a fixed vertical axis passing through its centre O with two point masses each of mass `(M)/(8)` at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is `(8)/(9) omega` and one fo the masses is at a distance of `(3)/(5) R` from O. At this instant the distance of the other mass from O is

A

`(2)/(3)R`

B

`(1)/(3)R`

C

`(3)/(5)R`

D

`(4)/(5)R`

Text Solution

Verified by Experts

The correct Answer is:
D
(d) Applying consersdvation of angular mumentum about
the axis
`MR^2 xx omega = MR^2xx(8omega)/(9) + (M)/(8) xx (9R^2)/(25)xx(8 omega)/(9) + (M)/(8) r^2 xx (8omega)/(9)`
`rArr r = (4r)/(5)`
D is the correct option
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs with one correct answer|1 Videos

  • MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|63 Videos

  • SIMPLE HARMONIC MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|69 Videos

Similar Questions

Explore conceptually related problems

A disc of mass m, radius r and carrying charge q, is rotating with angular speed omega about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment

A solid cylinder of mass M and radius R rotates about its axis with angular speed omega . Its rotational kinetic energy is

A ring of mass m and radius R is being rotated about its axis with angular velocity omega . If a increases then tension in ring

A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity omega . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be

A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity omega . Its kinetic energy is

A smoothh disc is rotating with uniform angular speed omega about a fixed vertical axis passing through its centre and normal to its plane as shown. A small block of mass m is gently placed at the periphery of the disc. Then (pickup the correct alternative or alternatives)

A thin circular ring of mass per unit length p and radius r is rotating at an angular speed omega as shown in figure. The tension in the ring is

A uniform rod of mass m and length l_(0) is rotating with a constant angular speed omega about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle theta to the vertical (axis of rotation).

A uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed omega in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is