Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length `l= sqrt(24a)` through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is `omega.` The angular momentum of the entire assembly about the point 'O' is `vecL` (see the figure). Which of the following statement (s) is (are) true?

Options

A. The centre of mass of the assembly rotates about the z-axis with an angular speed of `omega//5`
B. The magnitude of angular momentum of center of mass of the assembly about the point O is `81ma^2 omega`
C. The magnitude of angular momentum of the assembly about its center of mass is `17ma^2 omega//2`
D. the magnitude of the z-componet of `vacL is 55ma^2 omega.`

Answer

A, C

Explanation

(a,c) in `Delta OAM ,OM = sqrt(1^2 + a^2) = sqrt(2ha^2 + a^2) = 5a`
The circumference of a circle of radius OM will be `2pi(5a)
=10 pia.

For completing this circle once, the smaller disc will
have to take `(10 pia)/(2pia) = 5 rounds.`
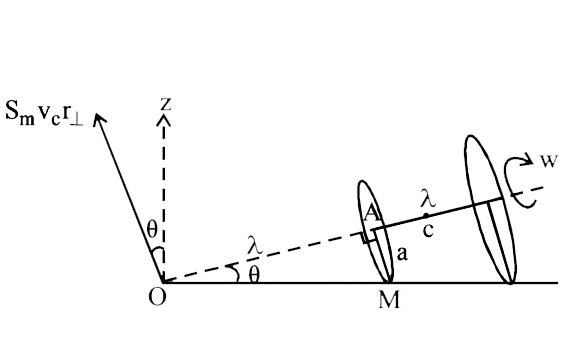
Therefore the C.M. of the assembly rotates about z-
axis with an angular speed of w/5.
The angular momentum about the C.M. of the system
`L_c = I_cw =[(1)/(2) ma^2] omega`
`+ [ (1)/(2)xx4mxx(2a)^2 ] xxomega = (17ma^2omega)/(2)`
Now ` v_c = (mxx omegaa+ 4m xx2 oemga)/(5m) = (9 omega a)/(5)`
and `r_|_ = (ml + 4mxx2I)/(5m) (9I)/(5)`
`L of C.M. = (5m xx 9omega a)/(5)xx(9I)/(5) = 81 m omega a^2 xx (sqrt24)/(5)`
`L_z = (81m omega a^2 sqrt24)/(5) cos theta -I_c omega sin theta`
`=81 m omega^2 sqrt((24)/(5))xx sqrt((24)/(5)) - (17ma^2omega)/(10)) = (1134)/(50) m omega a^2.`