A 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude `theta_0.` What is the tension in the rope when it makes en angle `theta` with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?

Answer

A, B, C

Explanation

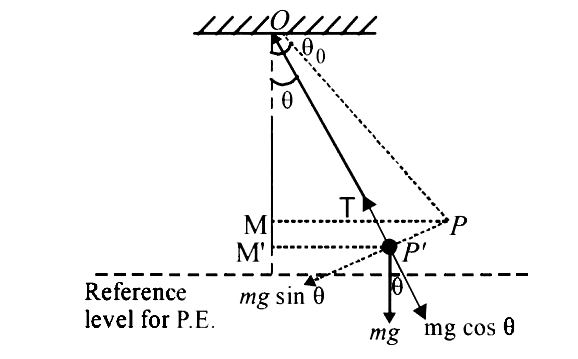
`T-mg cos theta = (mv^2)/(l)`
`:. T = (mv^2)/(l) + mg cos theta ….(i)`
In `Delta OPM, cos theta _0 = (OM)/(i)`
`rArr OM = I cos theta_0`
in `Delta OP'M',cos theta = (OM)/(i)`
`rArr OM = I cos theta `
`OM - OM = I (cos theta - cos theta_0)`
Loss in potential energy = Gain i kinetic energy
`rArr mgl (cos theta - cos theta_0) =(1)/(2)mv^2`
`rArr v^2 = 2gl(cos theta - cos theta_0)`
From (i) and (ii)
`T = (m)/(l) xx 2g l (cos theta - cos theta_0)+ mg cos theta`
`:. T = 3mg cos theta -2 mg cos theta_0`
`rArr T = mg (3 cos theta -2 cos theta_0)`
From equation (i) it is clear that the tension is maximum
when cos theta = 1i.e., theta = 0^@`
`:. T = mg`
Hence, `T_(max) = (mv^2)/(l) + mg ....(iii)`
From eqn.(ii)`
`v^2 =2gl(1-cos theta_0) ..(iv)`
From (iii) and (iv)
`T_(max) = (m)/(l) [2gl(1-cos theta_0)] + mg`
`:. T_(max) 3mg - 2mg cos theta_0`
`80 = 3xx40-2 xx40 cos theta_0`
`rArr 80cos theta_0 = 40 rArr cos theta_0 = (1)/(2) rArr theta_0 = 30^@.`