A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and `theta` is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

Answer

A, B

Explanation

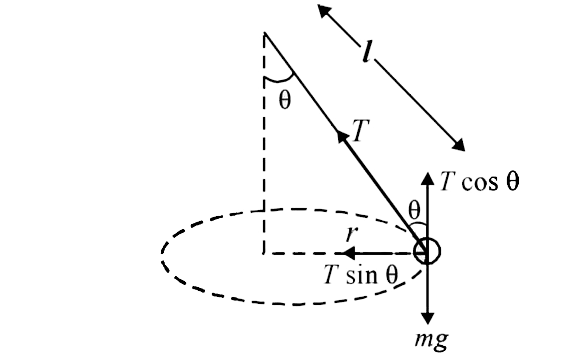
Suppose mass m moves around a circular path of radius r.
Let the string makes an angle `theta` with the vertical. Resolving
tension T, we get
and, `T sin theta = mr omega^2 …(i)
`T cos theta = mg….(ii)`
`:.tan theta = (romega^2)/(g)`
From diagram, sin theta = (r )/(l)`
`rArr r = l isn theta`
`:. tan theta = lsin theat (omega^2)/(g)`
`omega^2 = (tan theat.g)/(lsintheta) omega = sqrt((g)/(lcos theta))`
`rArr v = (1)/(2pi) sqrt((g)/(lcos theta)`....(iii)
From (ii), `T cos theta = mg.`
For M to remain stationary, T = Mg
`:. Mg cos theta = mg`
`rArr cos theta =(m)/(M) .....(iv)`
From (iii) and (iv) , v = (1)/(2pi)sqrt((g)/(l)(M)/(m))`