A circular plate of unifrom thickness has a diameter of `56 cm`. A circular portion of diameter `42 cm` is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

Answer

A, C, D

Explanation

Let `sigma` be the mass per unit area.
Then the mass of the whole disc `= sigmaxxpiR^2`
Mass of the portion removed `=simgaxxpir^2`
R = 28 cm: r =21 cm, OP = 7cm.

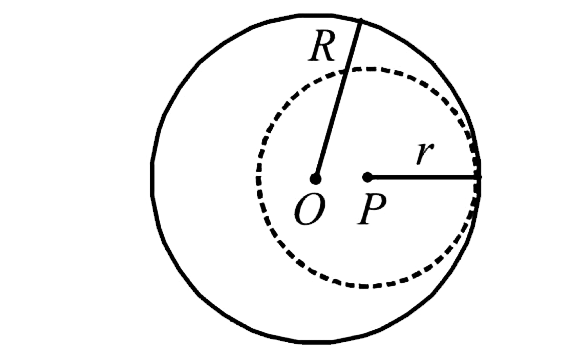
`x = (m_1x_1 - m_2x_2)/(m_1 - m_2)`
`=sigmaxxpiR^2(0) - sigmaxxpir^2 xx7)/(simga pi R^2 - sigma pi r^2)`
`=(-21)^2xx7)/((28)^2 - (21))^2 = - (21xx21xx7)/(7xx49) =- 9cm`
This means that the c.m. lies at a distance of 9cm from the
origin towards left.