A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

Answer

B

Explanation

C.M. of the system of two bodies in situation (i) in
x-coordinate
`x_C = (Mxx 0 +mx_1)/(M+m)` = (mx_1)/(M+m) …..(i)`


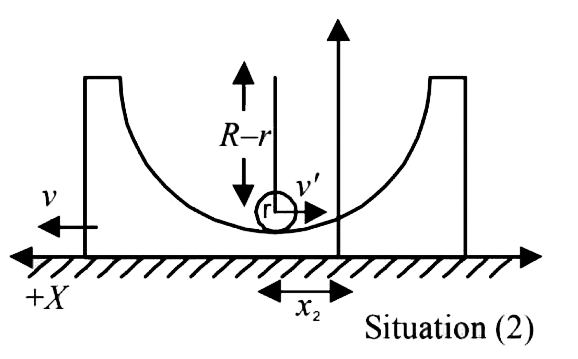
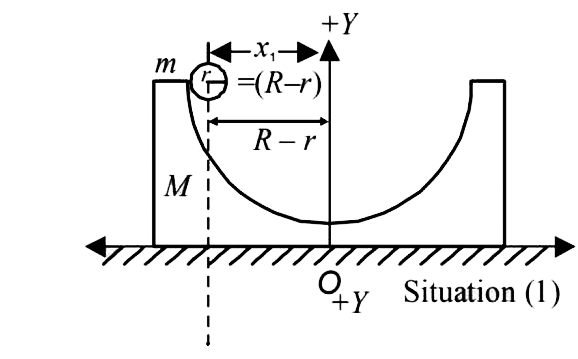
C.M. of the system in situation (ii) in x-coordinate is
`x'_C = (Mxx x_2+mxx x_2)/(M+m) = x_2 ....(ii)`
Since no external force is in x-direction
`:. x_C = x'_C `
`:. x_2 = (mx_1 )/(M + m) = (m(R-r)/(M +m)`
Applying conservation of linear momentum,
Initial Momentum = Final Momentum
`0 = MV - mv`
`:. v = (MV)/(m) ......(iii)`
Applying the concept of conservation of energy, we get
Loss in P.E. of mass m= Gain in K.E. of mass M and Gain in
K.E. of mass m
`rArr mg(R - r) =(1)/(2)MV^2 + (1)/(2)mv^2`
`rArr 2mg (R-r) = MV^2 + m(M^2V^2)/(m^2)` [from (iii)]`
`rArr 2mg (R - r) = MV^2 + (M^2GV^2)/(m)`
2mg(R -r)=MV^2 [(1+(M)/(m)] = MV^2 [(m+M)/(m)]`
`rARr (2m^2g(R -r)/(M(m+M) = v^2 rArr V =m sqrt(2g(R -r )/(M(m+M))`