A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination `30^@` to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s `10 rad s^(-1)` calculate the distance travelled by X from that instant of time until it comes to rest

Answer

A, B, C

Explanation

(i) The drum is given an initial velocity such that the block
X starts moving up the plane.

As the time passes, the velocity of the block decreases. The
linear retardation a, fo the block X is given by
`mg sin theta -T = ma .....(i)`
The linear retardation of the block and the angular
acceleration of the drum`(alpha)` are related as
`a = R alpha .....(ii)`1
where R is the radius of the drum.
The retarding torque of the drum is due to tension T is the
string.
`tau=TxxR`
But ` tau =Ialpha` where I = M.I. of drum about its axis of rotaion.
`:. TxxR = (1)/(2)MR^2alpha ......(iii) [:. I = (1)/(2)MR^2]`
From (ii) `TR = (1)/(2)MR^2 (a)/(R ) rArr a = (2T)/(M)`
Substituting this value in (i)`
`mg sin theta -T = m xx(2T)/(M) rArr mg sin theta = (1+(2m)/(M)T`
`:. T = (mg sin theta)xxM)/(M +2m) = (0.5xx9.8xxsin 30^@xx2)/(2+2xx0.5) = 1.63N`
(ii)The total kinetic energy of the drum and the block at
the instant when the dum is having angular velocity
`10 rads^(-1) gets converted into the potential energy of the
block

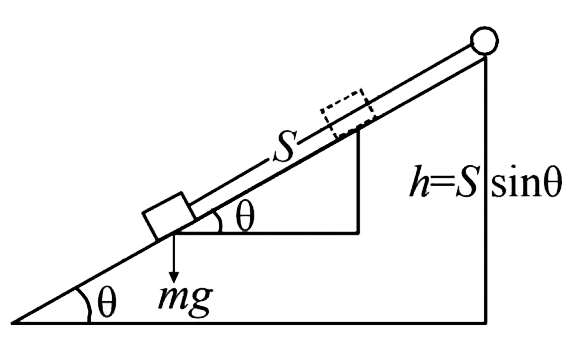
`[(K.E.)_(Rotational )]_(drum) + {(K.E)_(Translational)]_(block) = mgh`
`(1)/(2)Iomega^2 + (1)/(2)mv^2 = mgSsintheta`
`(1)/(2)I omega^2 + (1)/(2)m(Romega)^2 = mgS sin theta [:. v = Romega]`
`rArr (1)/(2)MR^2 omega^2+(1)/(2)mR^2 oemga^2 = mgS sin theta`
`rArr (1)/(2) (R^2oemga^2(M+m))/(mg sin theta) =S`
`rArr S = (1)/(2)xx(0.2xx0.2xx10xx10(2+0.5))/(0.5xx9.8xxsin 30^@) =1.22m`