Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.

Answer

C

Explanation

During collision, the torque of the system about P will be
zero because the only force acting on the system is through
P(namely weight of rods/mass m/reaction at P)
`Given: l =0.6m`
m_A 0.01kg`
`m_B = 0.02kg`
`m= 0.05kg`
since `tau = (dt)/(dt) and tau = 0`
`rArr L is constant.`

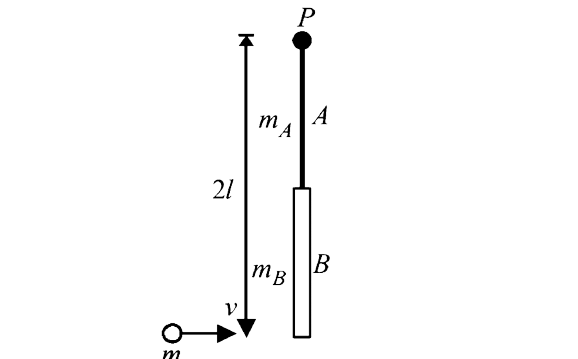
Angular momentum before collision `=mvxx2l ..(i)`
Angular momentum after collision `=iomega ..(ii)`
Where I is the moment of inertia of the system after collision
about P and `omega` is the angular velocity of the system. `M.I. about P:I_1 = M.I. of mass m`
`I_2 = M.I. of rod m_A`
`I_3 = M.I. of rod m_B`
`I=I_1+I_2+I_3`
`=[m(2l)^2 + {m_A((l^2)/(12)) + ((l)/(2))^2} + {m_B((l^2)/(12)) + ((l)/(2)+l)^2}]`
`=[4ml^2 + m_A((l^2)/(12)+(l^2)/(4)) + m_B ((l^2)/(12)+(9l^2)/(4))]`
`=[4ml^2 + (1)/(3)m_Al^2 +(7)/(3)mBl^2] = 0.09kgm^2`
Frm (i) and (ii)
`I oemga = mvxx2l`
`rArr omega = (mvxx2l)/(I) =(0.05xxvxx2xx0.6)/(0.09) = 0.67v`
Applying conservation of mechanical energy after collision.
(Using the concept of mass)
Loss of K.E. = Gain in P. E.
`(1)/(2)I omega^2 = mg(2l)+m_A((l)/(2))g +m_Bg((3l)/(2))`
`rArr (1)/(2)xx0.09xx(0.67v)^2`
`=[0.05xx2+0.01xx(1)/(2)xx(3)/(2)]xx9.8xx0.6`
`rArr v = 6.3m//s`