A wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity `-v hat`I towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. `Deltat,` during which the sphere exerts a constant force F on the wedge.

(a) Find the force F and also the normal force N exerted by the table on the wedge during the time `Deltat.`
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval `Deltat.`

Answer

A, B, C, D

Explanation

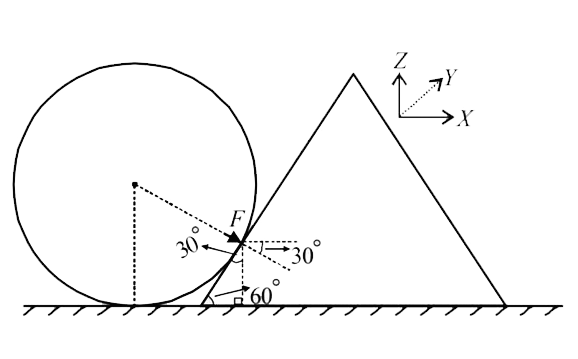
Resolving the force F acting on the wadge
`F_x = F cos 30^@, F_y = F sin 30^@`
The collison is elastic and since the spher is fixed,
the wadge will return back with the same velocity
(in magnitude).
The force responsible to change the velocity of the wedge
in X-direction is `Fx`
`F_x xx Delta t = mv - (-mv)`
(impulse) = (Change in momentum)
`:. F_x =(2mv)/(Delta t) rArr F cos 30^@ = (2mv)/(Deltat) rArr F = (4mv)/(sqrt3 Delta t)`
In vector terms
`vecF = F_x hati + F_y(-hatk) = F cos 30^@hati + F sin 30^@ (-hatk)`
`=Fxx(sqrt3)/(2)hati+Fxx(1)/(2) (-hatk)`
`rArr vecF = (F)/(2)(sqrt3 hati - hatk) = (2mv)/(sqrt3 Delta t) (sqrt3 hati - hatk)`
Taking equilibrium of force in Z-direction(acting on wadge)
we get
`F_y + mg = n`
`rArr N = (F)/(2) + mg = (2mv)/(sqrt3Delta t) + mg`
`N = ((2mv)/(sqrt3Delta t )+mg))hatk`
(b) Taking torques on wedge about the c.m. of lthe wedge.
Fxxh - Torque due to N+mgxx0 = 0
rArr Torque due to N = Fxxh = (4mv)/(sqrt3 Delta t) xxh`