A uniform circula disc has radius R and mass m. A particle also of mass m, is fixed at a point A on the edge of the disc as shown in figure. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially, the disc is held vertical with the point A at its highes position.

Explanation

KEY CONCEPT: During the fall, the disc-mass system gains
rotational kinetic energy. This is at the expense of potential
energy

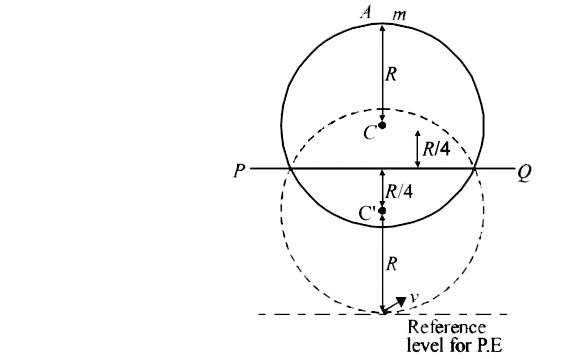
Applying energy conservation
Total energy initially = total energy finally
`mg((2R + (2R)/(4)) + mg ((R +(2R)/(4)) = mgR +(1)/(2) I oemga^2
Where I = M.I. of disc - mass system about PQ
`mgxx(10R)/(4) + mg(6R)/(4) = mgR +(1)/(2) Iomega^2 rArr 3mgR = (1)/(2)Ioemga^2`
`rArr omega = sqrt((6mgR)/(I)) .....(i)`
`(I)_PQ = (I_(disc))_PQ + (I_(mass))_PQ`
`=[(mR^2)/(4) + M((R )/(4))^2] + m ((5R)/(4))^2`
`[:. M.I. of disc about diameter = (1)/(4)MR^2]`
`(mR^2[4+1+25])/(16) = (15mR^2)/(8) ....(ii)`
From (i) and (ii)
`omega = sqrt((6mgRxx8)/(15mR^2)) = sqrt((16g)/(5R))`
Let v be the velocity of masss m at the lowest point of rotation
`v = omega((R +(R )/(4)) :. V = sqrt((16g)/(5R)) xx (5R)/(4) = sqrt(5gR)`