A man pushes a cylinder of mass `m_1` with the help of a plank of mass `m_2` as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
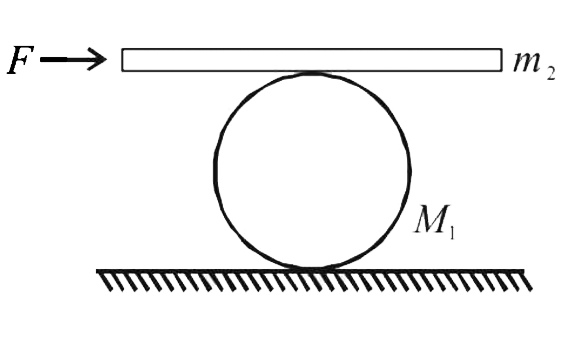
(b) the magnitudes and direction of frictional force at contact points.
A man pushes a cylinder of mass `m_1` with the help of a plank of mass `m_2` as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and

(b) the magnitudes and direction of frictional force at contact points.
(a) the acceleration fo the plank and the center of mass of the cylinder, and

(b) the magnitudes and direction of frictional force at contact points.
Text Solution
Verified by Experts
The correct Answer is:
A, B, C, D
The man applies a force F in the horizontal direction on the
plank as shown. Therefore the point of contact of the plank
with the cylinder will try to move towards right. Therefore
the friction force F will act towards left on the plank. To
each and every action there is equal and opposite reaction.
Therefore a frictional force f will act on the top of the cylinder
towards right.
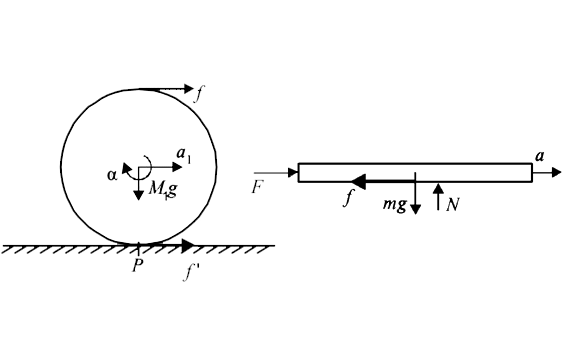
Direction of f' : A force f is acting on the cylinder. This force
is trying to move the point of contact P towards right by an
acceleration
`a_(cm) = (f)/(M_1) acting towards right.
At the same time, the force f is trying to rotate the cylinder
abuout its centre of mass.
`fxxR = Ixxalpha`
`rArr alpha = (fxxR)/(I) = (fxxR)/(1)/(2)M_1R^2 = (2f)/(M_1R)` in clockwise direction.
`:. alpha_(cm) + alphaR=(f)/(M_1) - (2f)/(M_1R) xxR = -(f)/(M_1,` i.e. towards left.
Therefore, the point of constact of the cylinder with the
ground move towards left. Hence frictin force acts towards
right on the cylinder.
NOTE: You ca assume any direction of friction at the point
of contact and solve the problem. If the value of friction
comes out to be positivem, our assumed direction is correct
otherwise the direction of friction is opposite. The above
activity is done so that if only the direction of friction is
asked, an approach may be developed.
Applying Newton's law on plank, we get
`F-f = m_2a_2 .....(i)`
Also, `a_2 = 2a_1 ...(ii)`
Because `a_2` is the accelration of topmost point of cylinder
and there is no slipping.
Applying Newton's no cylinder
`M_1a_1 = f+f ....(iii)`
The torque equation for the cylinder is
`fxx R - fxxR= Ialpha = (1)/(2)M_1 R^2xx((a_1)/(R ))`
`:. I = (1)/(2) M_1R^2 and Ralpha = a_1]`
`:. (f-f) R = (1)/(2) M_1Ra_1 rArr f+f=(1)/(2)M_1a_1 .....(4)`
Solving equation (iii) and (iv), we get
`f = (3)/(4)M_1a_1....(5)`
and `f = (1)/(4)M_1 a_1 ...(6)
From (i) and (iii)
`F - f=2m_2 a_1 rArr F- (3)/(4)M_1a_1 = 2m_2a_1`
`:. a_1 = (4f)/(3M_1+8m_2) :. a_2 = (8F)/(3M_1+8m_2)`
From (v) and (vi)
`f = (3)/(4)M_1xx(4f)/(3M_1+8m_2) = (3FM_1)/(3M_1+8m_2)`
and `f'=(1)/(4)M_1xxa_1 = (FM_1)/(3M_1+ 8m_2)`
plank as shown. Therefore the point of contact of the plank
with the cylinder will try to move towards right. Therefore
the friction force F will act towards left on the plank. To
each and every action there is equal and opposite reaction.
Therefore a frictional force f will act on the top of the cylinder
towards right.

Direction of f' : A force f is acting on the cylinder. This force
is trying to move the point of contact P towards right by an
acceleration
`a_(cm) = (f)/(M_1) acting towards right.
At the same time, the force f is trying to rotate the cylinder
abuout its centre of mass.
`fxxR = Ixxalpha`
`rArr alpha = (fxxR)/(I) = (fxxR)/(1)/(2)M_1R^2 = (2f)/(M_1R)` in clockwise direction.
`:. alpha_(cm) + alphaR=(f)/(M_1) - (2f)/(M_1R) xxR = -(f)/(M_1,` i.e. towards left.
Therefore, the point of constact of the cylinder with the
ground move towards left. Hence frictin force acts towards
right on the cylinder.
NOTE: You ca assume any direction of friction at the point
of contact and solve the problem. If the value of friction
comes out to be positivem, our assumed direction is correct
otherwise the direction of friction is opposite. The above
activity is done so that if only the direction of friction is
asked, an approach may be developed.
Applying Newton's law on plank, we get
`F-f = m_2a_2 .....(i)`
Also, `a_2 = 2a_1 ...(ii)`
Because `a_2` is the accelration of topmost point of cylinder
and there is no slipping.
Applying Newton's no cylinder
`M_1a_1 = f+f ....(iii)`
The torque equation for the cylinder is
`fxx R - fxxR= Ialpha = (1)/(2)M_1 R^2xx((a_1)/(R ))`
`:. I = (1)/(2) M_1R^2 and Ralpha = a_1]`
`:. (f-f) R = (1)/(2) M_1Ra_1 rArr f+f=(1)/(2)M_1a_1 .....(4)`
Solving equation (iii) and (iv), we get
`f = (3)/(4)M_1a_1....(5)`
and `f = (1)/(4)M_1 a_1 ...(6)
From (i) and (iii)
`F - f=2m_2 a_1 rArr F- (3)/(4)M_1a_1 = 2m_2a_1`
`:. a_1 = (4f)/(3M_1+8m_2) :. a_2 = (8F)/(3M_1+8m_2)`
From (v) and (vi)
`f = (3)/(4)M_1xx(4f)/(3M_1+8m_2) = (3FM_1)/(3M_1+8m_2)`
and `f'=(1)/(4)M_1xxa_1 = (FM_1)/(3M_1+ 8m_2)`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find (a) The acceleration of the centre of the cylinder (b) The friction force between the plank and the cylinder
A plank of mass m_1 with a uniform sphere of mass m_2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
A solid sphere of mass m and radius R is placed over a plank of same mass m . There is sufficient friction between sphere and plank to prevent slipping. When a horizontal force F is applied at centre of sphere, acceleration of the plank is
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Acceleration of the plank is
A sphere of mass m and radius r is placed on a rough plank of mass M . The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
A cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.
A solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact. (a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ? (b) Calculate the acceleration of the cylinder. (c ) Find the value of frictional force at A & B .
The mass m is placed on a body of mass M. There is no friction. The force F is applied on M on it moves with acceleration a. Then, the force on the top body is